Study showing how small errors in observations and models can impact predictability published in Chaos

This study uses a simple chaotic system to show that both model error and initial condition errors have profound impacts on predictability. These findings may have very important ramifications for how to design computer forecast models (and models in other fields where computer simulations are used) to improve their predictability. It is also shown for the first that small changes to the equations have a similar impact on the predictability limit as changes to the initial conditions, which can influence how sets of computer forecast models are designed and run.

This figure illustrates one of the key findings of the paper: in the presence of model error, the predictability of the logistic map has an upper limit. The black line is the situation with no model error, when the predictability limit continuously increases initial condition errors become smaller (toward the right).. But when model error is introduced (purple and green lines), growth of predictability limit is abruptly interrupted at certain initial condition error. The greater the model error (from the purple to the green line), the smaller is the upper limit of predictability.

Dynamical systems are equations that describe many phenomena around us, like aspects of human anatomy or the weather. Understanding these equations can therefore improve our ability to predict the phenomena.

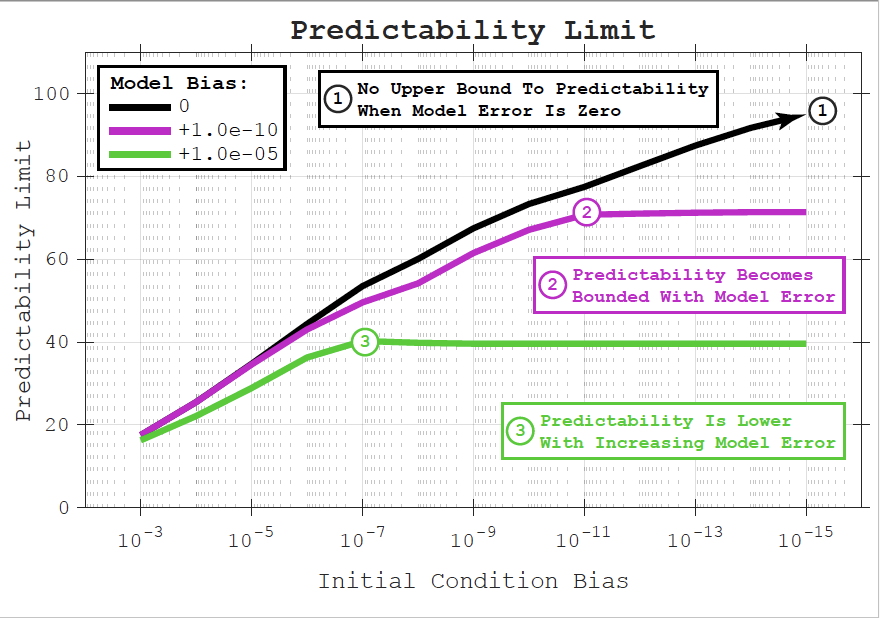
A key feature of dynamical systems is that they sometimes behave chaotically. When a system is chaotic, its behavior can change due to small differences in measurements of the system or to the equations themselves. This makes it especially challenging to make accurate predictions. A commonly used measure of chaos in dynamical systems is how far into the future we can reliably make predictions if there are small errors in how we describe what is currently happening, what we call initial conditions. This is known as the predictability limit of a system. In simple dynamical systems, it is generally expected the more accurately we can describe the initial conditions of the system and provide them to the equations, the longer it will take the simulation to develop large errors and for the system to become unpredictable. However, in very complex systems such as the weather, this isn’t the case. There is a characteristic predictability limit that we can’t extend even if we have extremely accurate initial conditions.

In this study, it is shown that the expectation that we can increase the predictability limit of a simple chaotic system through improved initial conditions doesn’t remain valid if the equations themselves are even slightly in error. This is demonstrated using the logistic map, a very simple dynamical system that only relies on a single parameter (a number used in the logistic map’s equation that controls the system’s behavior). If this parameter is known perfectly, the predictability limit can be extended indefinitely through more accurate initial conditions, as expected. However, if the parameter has even the slightest error, this behavior abruptly changes, and we can no longer extend predictability indefinitely by making initial condition errors smaller.

All models have errors, since they are, after all, just equations we use to explain the real systems they try to predict. If predictability is critically dependent on not just initial conditions but also model accuracy even in the simplest dynamical systems, it follows that efforts to improve weather forecasts should not just focus only on better observations (both in accuracy and coverage) but also on the betterment of the models themselves.

■ Important Conclusions:

If there is no model error, the predictability limit of the logistic map can be extended continuously by reducing initial condition error.
When model error is introduced, the predictability limit becomes smaller. Furthermore, a fundamental change occurs where the predictability limit cannot be extended by further by improving the initial conditions. Increasing predictability beyond this requires also lowering errors in the model equations, such as by improving model parameters.
Because small changes to initial conditions can lead to large forecast changes, weather forecasters use ensemble forecasts, or groups of computer forecasts starting at the same time with small differences in initial conditions that might occur due to errors or gaps in our measurements. This gives forecasters a range of likely possible outcomes which can be used to make forecasts even when predictability becomes small. Specifying initial condition differences that are of the right size is critical to making these forecasts and extending the predictability limit.
There are multiple ways that ensemble forecasting systems can be designed to extend predictability. Understanding how initial and model errors interact is necessary to optimally design these systems.

For more information, contact aoml.communications@noaa,gov. Funding support was provided through the Cooperative Agreement NA67RJ0149 between NOAA and the University of Miami, and the author is grateful to have been able to carry out this work without other external financial support under the auspices of University of Miami’s Cooperative Institute for Marine and Atmospheric Studies. The full text can be found at https://pubs.aip.org/aip/cha/article/34/1/011102/3261410/A-Monte-Carlo-approach-to-understanding-the.