WMO/CAS/WWW
FIFTH INTERNATIONAL WORKSHOP on TROPICAL CYCLONES
Topic 3.4: Theoretical advancements
Rapporteur: Johnny Chan
Laboratory for Atmospheric Research
Dept. of Physics & Mat. Sci.
City University of Hong Kong
Kowloon, Hong Kong, China
E-mail: johnny.chan@cityu.edu.hk
Fax: 852-2788-7830
Abstract:
Compared with the last few Workshops, the amount of research work to be reported here is much smaller because only a few papers have been published in the area of the theory of tropical cyclone motion since the last International Workshop on Tropical Cyclone. The main focus of the researchers has been on the application of the concept of potential vorticity tendency. The main result is that a tropical cyclone tends to move towards an area of maximum azimuthal wavenumber-1 potential vorticity tendency, which is mainly contributed by the horizontal advection of potential vorticity and diabatic heating. Based on the results from modeling studies and observational analyses, this concept appears to work in many types of tropical cyclone motion. However, whether such a concept works for other sub-synoptic scales of motion requires further investigation.
3.4.1. Introduction
Since the Fourth International Workshop on Tropical Cyclones (IWTC-IV), the number of papers devoted to the study of the theory of tropical cyclone (TC) motion has dwindled significantly. In fact, a search through the database shows less than 10 papers have been published in this area since 1998. This suggests that within the last decade or so, our understanding of TC motion has advanced so much that most scientists working in this area have shifted their attention to other topics. In the rapporteur report for first IWTC, the discussion on the theory of TC motion focused on the linear beta-effect (Holland 1985). Then, results from barotropic studies dominated the reports in IWTC-II and III (Carr 1989; Chan 1993 respectively) although some baroclinic investigations had already started between the two workshops (Chan 1993). By IWTC-IV, the importance of understanding baroclinic processes in TC motion was highlighted (Wang 1998). Reports on barotropic processes mostly focused on consolidation of the ideas and concepts. In other words, to a large extent, the community has apparently reached a consensus on the physical mechanisms responsible for TC motion from a barotropic perspective.
Wang’s (1998) report and an earlier summary by Elsberry (1995) have provided excellent reviews of the “state of science” of our understanding of baroclinic processes related to TC motion up to 1998. Therefore, this report will only focus on developments since then, which consists of studies based on the potential vorticity perspective.
3.4.2. The potential vorticity tendency approach
In many studies involving the use of potential vorticity (PV) prior to 1999, the inversion technique (Hoskins et al. 1985) was often employed to obtain wind and mass fields to explain TC motion. A difficulty in such an approach is that the technique depends critically on the vertical stability of the atmosphere. In other words, different assumptions can lead to different results, which leads to a problem of interpretation as to whether the result is physical. Wu and Wang (2000, hereafter WW) therefore proposed instead to study TC motion based on the time tendency of PV, which is an extension of the barotropic idea of Chan (1984) who related TC motion to the tendency of relative vorticity.
WW’s approach is to assume a TC circulation being dominated by its symmetric component, which is likely true to a large extent. Based on this assumption, they showed that a TC tends to move towards an area of maximum azimuthal wavenumber-1 (WN1) PV tendency (PVT) so that
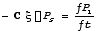 , (3.4.1)
, (3.4.1)
where C is the TC motion vector, Ps and P1 the symmetric and WN1 components of PV respectively. Therefore, by identifying the location of maximum _P1/_t, the motion of the TC can be determined. WW demonstrated that by using a least-squares approach, the value of C can be estimated, which was close to the predicted motion of the vortex in their model.
Many physical processes can contribute towards the PVT, which can be grouped symbolically into four terms (WW and Chan et al. 2002):
 , (3.4.2)
, (3.4.2)
where _1 is an operator that extracts the WN1 component. WW showed in their numerical study of a vortex on a beta plane without a background flow that the contributions to the motion of the model vortex in the mid troposphere are mainly from the horizontal advection and diabatic heating term. In the absence of diabatic heating, the horizontal advection becomes the dominant term with the vertical PV advection associated with the asymmetric vertical motion playing a secondary role (Wu and Wang 2001a). A further breakdown of the heating term shows that the asymmetric component of diabatic heating tends to cause a vortex to move towards a region of maximum downward gradient of asymmetric heating (Wu and Wang 2001b). The level at which the asymmetric heating vanishes can be called the “steering level” since at this level, the model vortex moves with the areal-mean asymmetric flow near the TC center.
Chan et al. (2002) attempted to use the approach of WW to explain the motion of actual TCs. They found that the diabatic heating term appears to be important in slow-moving TCs and those with oscillatory motion or sudden track changes. Otherwise, the horizontal advection term is generally dominant. A breakdown of this latter term suggests that although the advection of symmetric PV by the asymmetric flow is usually dominant, the advection of asymmetric PV by the symmetric flow also contributes to the overall motion. The sum of these two components aligns with the direction of TC motion much better than either one alone. They also found that in a recurving case, the location of the maximum PVT contributed by the advection terms rotates ahead of the turning motion of the TC, a result also found by Chan (1984) based on the concept of absolute vorticity conservation. It should further be noted that because the contribution of heating towards motion is through its horizontal gradient, the motion vector was found in many cases to be towards the edge of the heaviest convection, a result previously found by Lajoie (1976) from examination of satellite pictures. The idea that rotation of convective heating can lead to a turning of a TC has also been shown by Willoughby (1988, 1992) in idealized simulations.
Thus, both numerical and observational studies appear to give consistent results when using the PVT approach. That is, the motion of a TC apparently follows the area of maximum azimuthal WN1 PVT, which is contributed by mainly the horizontal advection and diabatic heating terms. The relative contributions from each of the terms depend on individual cases.
In barotropic studies of TC motion (i.e. applying the concept of absolute vorticity conservation), the beta effect has to be explicitly calculated. However, using the PVT approach, the beta effect becomes implicit in the equation since the meridional variation of planetary vorticity contributes towards a horizontal (asymmetric) PV gradient. In other words, it is not necessary to isolate this effect. This has the advantage that the sometimes-opposing contributions from vertical wind shear (which also gives rise to a horizontal PV gradient) and the beta effect (Shapiro 1992) do not have to be treated separately.
Wu and Wang (2001a) and Chan et al. (2002) decomposed the WN1 component of the horizontal advection (HA) term to understand better the physical processes involved. That is,
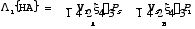 (3.4.3)
(3.4.3)
where the subscripts s and 1 indicate the symmetric and WN1 components. At first glance, Term A appears to be the contribution from the steering flow. However, it actually represents more than one process. Other than the environmental flow (i.e., the traditional concept of steering), V1 also contains the “ventilation flow” associated with the beta effect and any other asymmetric flow that may develop (e.g. due to asymmetric convection). In addition, while Ps is largely equal to the PV of the vortex, any symmetric component of the environmental PV as well as symmetric convection will also have a contribution. Term B represents the symmetric advection of asymmetric (i.e. WN1) PV. The WN1 PV consists of the beta gyres, other asymmetric features in the environmental flow such as vertical shear, as well as contributions from asymmetric convection. Indeed, Wu and Wang (2001b) found that the asymmetric heating represents a significant contribution in many cases. Note that the symmetric flow contains both the vortex circulation and the symmetric component of the environmental flow.
It should also be pointed out that the diabatic heating term depends on the vertical and horizontal variations of convective heating, as well as vertical shear (WW). In other words, the contribution of heating term towards WN1 PVT is not simply through convective heating.
3.4.3. Research issues
It appears that applying the concept of PVT can largely explain TC motion. However, even though Chan et al. (2002) examined more than 300 cases, certain assumptions were necessary in estimating the PVT. Furthermore, the large-scale circulation often does not have enough resolution to provide better estimates especially when the convective asymmetries are in the form of mesoscale convective systems (MCS) that have relatively small spatial scales. Thus, to determine whether the PVT approach applies in these cases would require high-resolution data, which may be difficult to obtain unless another field experiment is conducted.
Another problem is oscillatory motion. This could be the type of meandering or stepping motion on a relatively large scale (e.g. Yancy 1990; Rex 1998, both in the western North Pacific), or small-scale oscillation that occurs especially near landfall. Whether such motion can be explained by the PVT approach remains to be seen particularly in landfall situations as contributions from frictional processes become important.
So far, most modeling studies assume a constant sea-surface temperature (SST). What effect would variations of SST have on TC movement? Would a air-sea coupled model be necessary to study such effects? How would such effects be verified from observations?
3.4.4. Summary
Research on the theory of tropical cyclone motion has not been very active since the last International Workshop on Tropical Cyclones in 1998. Nevertheless, the recent work of a couple of groups (University of Hawaii and City University of Hong Kong) have apparently came to the same conclusion (using numerical modeling and observational analyses respectively) that potential vorticity tendency can be used both as a diagnostic and a prognostic tool for identifying the motion of a tropical cyclone. Specifically, a tropical cyclone tends to move towards an area of maximum azimuthal wavenumber-1 potential vorticity tendency, which is mainly contributed by the horizontal advection of potential vorticity and diabatic heating. To the extent allowed by the assumptions in the model and in the observational analyses, this concept appears to work in many types of tropical cyclone motion.
Questions, however, remain as to whether this concept can also be applied to interaction of the tropical cyclone with mesoscale convective complexes or sub-synoptic scale of motion such as oscillatory motion. The contribution of an interactive ocean also needs to be ascertained. These problems may form the future research work on the theory of tropical cyclone motion.
References
Carr, L. E., III, 1989: Advances in Basic Understanding of Tropical Cyclone Motion. Rapporteur Report, Topic 2.2, 2nd WMO International Workshop on Tropical Cyclones, Tech. Doc. WMO/TD-No. 319, WMO, Geneva, Switzerland, 2.2.1-2.2.18.
Chan, J. C. L., 1984: An observational study of the physical processes responsible for tropical cyclone motion. J. Atmos. Sci., 41, 1036-1048.
Chan, J. C. L., 1993: Research Rapporteur Report on Tropical Cyclone Motion. Rapporteur Report, Topic 4.1, 3rd WMO/ICSU International Workshop on Tropical Cyclones, Tech. Doc. WMO/TD-No. 573, WMO, Geneva, Switzerland, 57-66.
Chan, J. C. L., F. M. F. Ko and Y. M. Lei, 2002: Relationship between potential vorticity tendency and tropical cyclone motion. J. Atmos. Sci., 59, 1317-1336.
Holland, G. J., 1985: Theories of Tropical Cyclone Motion. Rapporteur Report, Topic 5.5, WMO/CAS International Workshop on Tropical Cyclones, Tech. Doc. WMO/TD-No. 73, WMO, Geneva, Switzerland.
Hoskins, B. J., M. E. McIntyre and A. W. Robertson, 1985: On the use and significance of isentropic potential vorticity maps. Quart. J. Roy. Meteor. Soc., 111, 877-946.
Lajoie, F. A., 1976: On the direction of movement of tropical cyclones. Aust. Meteor. Mag., 24, 95–104.
Shapiro, L. J., 1992: Hurricane vortex motion and evolution in a three-layer model. J. Atmos. Sci., 49, 140-153.
Wang, B., 1998: Baroclinic Processes. Rapporteur Report, Topic 3.2, 4th WMO International Workshop on Tropical Cyclones, Tech. Doc. WMO/TD-No. 875, WMO, Geneva, Switzerland, 3.2.1-3.2.6.
Willoughby, H. E., 1988: Linear motion of a shallow-water, barotropic vortex. J. Atmos. Sci., 45, 1906–1928.
Willoughby, H. E., 1992: Linear motion of a shallow-water barotropic vortex as an initial-value problem. J. Atmos. Sci., 49, 2015–2031.
Wu, L.-G. and B. Wang, 2000: A potential vorticity tendency diagnostic approach for tropical cyclone motion. Mon. Wea. Rev., 128, 1899–1911.
Wu, L.-G. and B. Wang, 2001a: Movement and vertical coupling of adiabatic baroclinic tropical cyclones. J. Atmos. Sci., 58, 1801-1814.
Wu, L.-G. and B. Wang, 2001b: Effects of convective heating on movement and vertical coupling of tropical cyclones: A numerical study. J. Atmos. Sci., 58, 3639-3649.
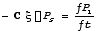 , (3.4.1)
, (3.4.1) , (3.4.2)
, (3.4.2)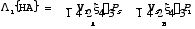 (3.4.3)
(3.4.3)