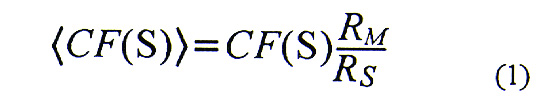
Authors
Richard J Murnane, Chris Barton, Eric Collins, Jeffrey Donnelly, James
Elsner, Kerry Emanuel, Isaac Ginis, Susan Howard, Chris Landsea, Kam-Liu,
David Malmquist, Megan McKay, Anthony Michaels, Norm Nelson, James O'Brien,
David Scott, and Thompson Webb III
For more information, contact Richard J. Murnane, Risk Prediction Initiative, Bermuda Biological Station for Research, Ferry Reach, St. George's, GE01, Bermuda;
In the United States, intense hurricanes (category 3,4, and 5 on the Saffir/Simpson scale) with winds greater than 50ms' have caused more damage than any other natural disaster [Pielke and Pielke, 1997]. Accurate estimates of wind speed exceedance probabilities (WSEP) due to intense hurricanes are therefore of great interest to (re)insurers, emergency planners, government officials, and populations in vulnerable coastal areas.
The historical record of US. hurricane landfall is relatively complete only from about 1900, and most model estimates of WSEP are derived from this record. During the 1899-1998 period, only two category-5 and 16 category-4 hurricanes made landfall in the United States. The historical record therefore provides only a limited sample of the most intense hurricanes.
In addition, our knowledge of the location and maximum wind of any hurricane becomes less certain the earlier it occurred in the record. As a result, in many instances, the historical record is not adequate for the development of precise and accurate model-based estimates of WSEP for an intense hurricane reaching.
However, geologic records can provide independent estimates of the probability of intense hurricane landfall. Such records are currently the only way of independently testing the probabilities of extreme wind events predicted with models based on historical data.
To date, the most useful proxy for intense hurricane landfall is sand layers in coastal lakes and marshes deposited by overwash processes associated with storm surge. The three-dimensional structure of the sand layers in marsh and lake sediments is determined by analyzing a suite of sediment cores. The relationship between sand layer geometry and wind speed is calibrated using sand layers produced by storms with known wind speeds that have passed near the coring sites. The sand layer chronology is usually determined using radioisotope data, often 14C dates of organic material adjacent to the sand layer.
The annual exceedance probability for winds equal to those associated with the calibration storm is set equal to the reciprocal of the average time interval between sand layers of a size equal to or larger than the reference layer.
Model Development Workshop
Given these constraints, what, then, is the annual probability of hurricane winds exceeding 50 ms-1, at a point along the East or Gulf coasts of the United States? How can one estimate and verify the annual probability of an event that has never occurred in the historical record; for example, hurricane winds above 60 ms-1, near New York City?
These are two of the many questions of great interest to the insurers that sponsor the Risk Prediction Initiative (RPI), a not-for-prof it science-business partnership funded by a consortium of (re)insurance companies, based at the Bermuda Biological Station for Research (see http://www.bbsr.edu/rpi/).
The RPI held a workshop in July 1997 to address these difficult questions. The goal was to develop a model algorithm for estimating the WSEP of hurricanes at landfall that could be verified with independent data from the geologic record. The remainder Of this article discusses the development of such a model.
Description of Model
The model requires two data sets: one specifies the latitude and longitude of the coastline, and the second gives the maximum wind speed and location (latitude and longitude) of a hurricane crossing the coastline. The model uses a least squares fit of exponential and/or power law equations to quantify for a given location, the relationship between exceedance wind speed, and the cumulative frequency of hurricane wind speeds at landfall. Using this relationship and the time span of the observational record, the model produces a coastline map showing the probability of winds exceeding a specified speed and a graph of WSEP for a specified location.
The model algorithm used to calculate landfall probabilities is straightforward. After the model reads the wind speed and coastline data sets, the user specifies several parameters that are needed for the calculation. Two of these parameters should vary as a function of location to calculate the most appropriate probability estimates. The first is the wind speed, SB, that will be used as the boundary dividing the power law and exponential equations.
Generally, a single exponential relationship adequately fits the data. In some locations, however, there is a change in slope in between the cumulative frequency versus exceedance wind speed relationship, so that two equations are needed to adequately model the data.
The change in slope, which commonly occurs at wind speeds of ~ 40-50 ms-1, may be an artifact of a storm's forward motion , or could be related to such effects as concentric eyewall formation, which strongly affects hurricanes with winds near 40-50 ms-1 [Willoughby, 1990].
The second parameter is the search radius, Rs, around a given point. The size of Rs, is a compromise between sample size and local representation. That is, Rs should be large enough to retain a sufficient number of storms adequate to develop confidence intervals via bootstrap re-sampling, but small enough to reduce the influence of storms that do not represent local storm characteristics.
Additional model parameters that must be set by the user include the number of years represented in the wind speed data set, the time interval for which wind speed exceed- probabilities should be calculated, the exceedance wind speed for the probabilities used to construct a map (see below), and the radius of maximum winds for a hurricane. Finally the user must decide if the probabilities will be based directly on the winds in the local data set, or if a correction will be made for the reduction in wind speed with increasing distance from a storm.
Once the parameters are set, the model develops a local wind speed data set by searching the wind speed data set for storms within a distance Rs of a given point. This local wind speed data set is then used to calculate a relationship between wind speed (S) and the cumulative frequency of winds exceeding S,CF(S).
If the user chose to use the maximum wind speeds directly, then CF(S) for the local storm set must be normalized to account for the effects of a variable search area. (CF(S) will increase with Rs .) We choose to normalize by the factor Rm / Rs, where Rm is the radius of maximum winds. The normalized cumulative frequency <CF(S)>, is therefore related to the cumulative frequency, CF(S), of storms by the relationship
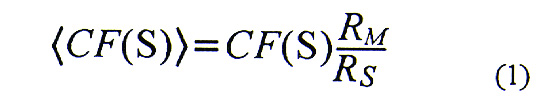
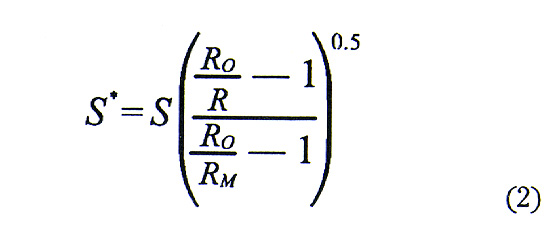
The storms associated with a given point are then divided into two sets based on whether their wind speed is faster or slower than SB. Winds slower than SB. are assumed to follow the power-law relationship
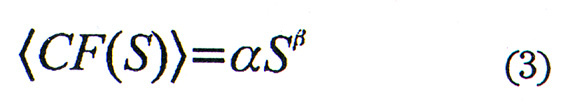
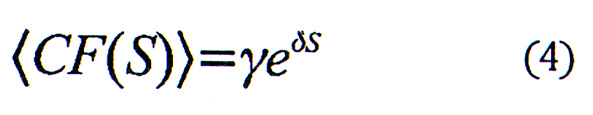
The coefficients from the least-squares fits are then used to calculate a predicted cumulative frequency <CF(S)>*, at each wind speed represented in the original data set. The 5% and 95% confidence intervals for <CF(S)>* based on the power law and exponential equations are determined using a bootstrap strategy. The model sets an upper limit for wind speeds at 95 ms-1 (~185 knots). This value exceeds the highest maximum sustained winds ever observed in a tropical cyclone (85 ms-1, Typhoon Tip in the northwest Pacific, October 12,1979).
The model next calculates the probability P of equaling or exceeding a wind speed during a specified time interval, Δt. The leastsquares fit of the scaling laws provides the expected number of events, <CF(S)>*, that equal or exceed a wind speed, S. If we divide <CF(S>* by the time span of the landfall data set,Εt, we then have an annual probability, p, of winds that equal or exceed S:
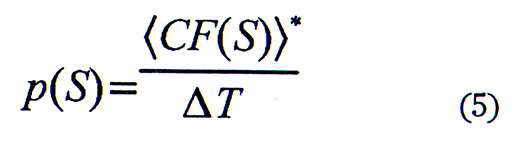
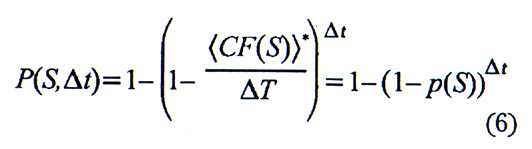
Model estimates of the probability of the U.S. coastline experiencing hurricane winds exceed- 50 ms-1 during a 5-year period are shown in Figure 1. The map is constructed by repeating the previous procedure, except for the bootstrap, at each point along a coastline. The model also can produce exceedance probability plots with 5% and 95% confidence intervals for any point along the coastline (Figure 2).
Model Data Sets
Model can predict WSEP for any coastline, given a properly formatted coastline (latitude and longitude) and wind speed (latitude, longitude, and wind speed at landfall) data set.
A variety of issues must be considered when developing a wind speed data set. For example, does one include multiple coastal crossings by a single storm? How does one handle storms that nearly reach land, move parallel to a coastline, or re-emerge to the ocean following landfall?
Such issues introduce a subjective component into landfall data sets. For this study wind speed, latitude, and longitude of tropical cyclone landfall were extracted from the National Hurricane Centers (NHC's) North Atlantic hurricane database (HURDAT) [Jarvinen et al., 1984], which is maintained and updated by the U.S. National Hurricane Center (http://www.nhc.noaa.gov/pastall.html). The landfall record includes storms from 1900-1997, multiple landfalls by a single storm, and crossings from land to sea if winds were greater than ~35 ms-1.
It also includes storms that nearly make landfall and it selectively chooses landfall sites for storms that parallel the coastline. The extracted wind speeds are mainly the values listed at the last 6-hour interval before landfall. The latitude and longitude of landfall are sometimes interpolated to the coastline when a storm is moving rapidly toward shore.
The intensity and number of storms in this landfall data set differ from other compilations. For example, there are a similar number of total storms but fewer intense hurricanes than a data set based on hurricane central pressures [Neumann et al., 1999]. The reasons for the discrepancies are threefold.
First, the HURDAT data [Jarvinen et al.,
1984] have maximum winds listed only for every 6 hours of a hurricane's
lifetime, not at the exact time of landfall. Second, the HURDAT data for
the first few decades of this century were oncedaily estimates that were
subsequently interpolated rather crudely down to 6-hourly values. Finally,
there is no simple one-to-one relationship between the maximum wind speed
in a storm and its central pressure.
Comparison of Model Predictions with Proxy Data
Three examples of proxy-derived estimates of WSEP aptly illustrate the potential value and limitations of using geological records of hurricane landfall (Figure 2). The records are from Western Lake, a coastal lake in the Florida panhandle [Liu and Fearn, 1997]; Singleton Swash, a fresh water marsh in South Carolina [Scott et al., 1991; and Succotash Marsh, a coastal marsh in Rhode Island [Bravo et al., 1997]. In each example, we compare the model predictions based on the maximum winds with the proxy-derived estimates.
At Westem Lake,Fla., which yields a proxy hurricane record spanning the last 5,000 years, there is good agreement between the proxybased estimate and the model prediction of the probability of exceeding category-4 winds (59 ms-1, Figure 2a), as both suggest about a 0.35% probability of occurrence per year. The agreement between proxy- and model-estimated probabilities at West- Lake increases our confidence in the model derived estimates of the probability of winds in this region exceeding those associated with a specific hurricane intensity category
At the Singleton Swash, S.C., site (Figure 2b) the proxy-based estimate (0.45% probability of occurrence per year) is in good agreement with the model predictions. Here, the proxy-based estimate likely represents a lower bound on landfall probabilities of category-3 or greater storms because of difficulties in developing a landfall record from cores at this site [Scott et al, 1999]. Scott et al. [ 1999] use the presence of offshore foraminifera to verify the origin of sand layers in the coastal pond and to record the landfall of a major hurricane when sand layers are absent from a core.
Proxy-based estimates of the probability of category-3 or greater winds in Succotash Marsh, R.I. (Figure 2c,0.74% probability of occurrence per year), far exceed the model predictions when the maximum winds are used directly. The geologic record includes storms back to ~1400 A.D. The higher storm frequency in the geologic record is probably not due to winter storms (Nor'easters) in the region, because the storm surge associated with these events is not sufficient to produce overwash deposits at this site [U.S. Army Corps of Engineers, 1962].
Additional support for the proxy-derived probability comes from historical reconstructions of storms back to 1635. Three intense hurricanes have crossed near Succotash Marsh since 1635 [Boose et al., 1997]. This implies a landfall probability of 3/363 = 0.008 (diamond in Figure 2c) consistent with the longer proxy-based record. A better fit between model- and proxy-based estimates of wind speed exceedance probability is found when the winds are corrected for their decay with distance from a storm (Figure 2d). In this case, the proxy record suggests that the model with the greater probability estimates provides a better estimate of wind speed exceedance probabilities.
Many proprietary models estimate the probability of extreme winds due to a hurricane. However, the only public model of which we are aware is the HURISK model developed by the National Hurricane Center [Neumann, 1987). Many, if not all, of these models share a common set of problems. For example, there are usually no confidence intervals for the probability estimates; the precision and accuracy of the probability estimates for rare and extreme winds are limited by the short historical record; and the probability estimates for extreme winds have not been verified by independent data.
Our model directly addresses one of these problems by incorporating confidence intervals for WSEP We also use geologic data to provide an independent check on model predictions. For example, the use of geologic data from Succotash Marsh provides a basis for accepting one model result over another. The Risk Prediction Initiative is also funding work at other locations to determine the probability of experiencing intense hurricane winds in regions, such as the Mid-Atlantic coast of the United States, that have not experienced intense hurricane winds over the last 100 years.
Independent estimates of wind speed exceedance probabilities are needed for many locations along the U.S. Gulf and East coasts, and along coastlines in other areas around the world that are subject to tropical cyclone landfall information can be used not only to validate risk models used by (re)insurers, but also to assess how tropical cyclone landfall frequency changes in response to natural climatic variability on centennial-to-millennial time scales, and to test the ability of high-resolution global general circulation models to predict changes in landfall frequency due to natural climate variability on these time scales.
Acknowledgments
This work was funded by the sponsors of the Risk Prediction Initiative at the Bermuda Biological Station for Research, Inc. Java programming support for the model was provided by Instrumental Software Technologies, Inc. (http://www.isti.com).
Authors
Richard J Murnane, Chris Barton, Eric Collins, Jeffrey Donnelly James Elsner Kerry Emanuel, Isaac Ginis, Susan Howard, Chris Landsea, Kam- Liu, David Malmquist, Megan McKay, Anthony Michaels, Norm Nelson, James O'Brien, David Scott, and Thompson Webb III For more information, contact Richard J. Murnane, Risk Prediction Initiative, Bermuda Biological Station for Research, Ferry Reach, St. George's, GE01, Bermuda; E-mail: rmurnane@bbsr.edu
References
Boose, E. R., K. E. Chamberlin, and D. R. Foster, Reconstructing historical hurricanes in New England, 22nd Conference on Hurricanes and Tropical Meteorology, Ft. Collins, Colo., Am. Meteorol. Soc., 388--389,1997.
Bravo, J., J. P. Donnelly and T.Webb III, Sedimentary evidence for the 1938 hurricane in southern New England, 22nd Conference on Hurricanes and Tropical Meteorology, Fort Collins, Colo., Am. Meteorol. Soc., 395--396,1997.
Jarvinen, B. R., C. J. Neumann, and M. A. S. Davis, A tropical cyclone data tape for the North Atlantic Basin, 1886-1983: Contents, limitations, and uses, NOAA Tech. Memo., , NWS NHC 22, Coral Gables, Fla., 21 pp., 1984.
Liu, K. B., and M. . L. Fearn, Lake sediment records of Hurricane Opal and prehistoric hurricanes from the Florida Panhandle, 22nd Conference on Hurricanes and Tropical Meteorology, Am. Meteorol. . Soc., Fort Collins, Colo., 397-398,1997.
Neumann, C. J., The National Hurricane Center Risk Analysis Program (HURISK), NOAA Tech. Memo., NWS NHC 38, Coral Gables, Fla., National Hurricane Center, 1987.
Neumann, C. J., B. R. Jarvinen, CA. McAdie, and G. R. Hammer, Tropical Cyclones of the North Atlantic Ocean, 1871-1998, Historical Climatology Series 6- 2, prepared by the National Climatic Data Center, Asheville, N.C., in cooperation with the Tropical Prediction Center/National Hurricane Center, Miami, Fla., 206 pp., 1999.
Pielke Jr., R. A., and R. A. Pielke Sr., Hurricanes: Their Nature and Impacts on Society, John Wiley and Sons Press, London, 279 pp., 1997.
Scott, D. B., E. S. Collins, PT, Gayes, and E. Wright, Hurricane records on the South Carolina coast: Patterns of periodicity over the last 5000 years (abstract), Annual Geological Society of America Meeting, Denver, Oct. 1999, , p. 13 1, A382.
U.S. Army Corps of Engineers, Water Resources Development, Interim Report, , Point Judith, R.I, Appendices, U. .S. Army Engineer Division, Waltham, Mass., 1962.
Willoughby, H. .E., Temporal changes of the
primary circulation in tropical cyclones, J. Atmos. Sci., 47, 242-264,1990.