WMO/CAS/WWW
FIFTH INTERNATIONAL WORKSHOP on TROPICAL CYCLONES
Topic 1 TROPICAL CYCLONE STRUCTURE AND STRUCTURE CHANGE
[Russ Elsberry (USA)]
Topic 1.1 Observations
Rapporteur: Dr. Frank Marks (USA)
NOAA/HRD
4301 Rickenbacker Causeway
Miami, FL 33149 USA
E-mail: Frank.Marks@noaa.gov
Fax: 1 305.361.4402
Working Group: R. Hood, Y. Yong, F. Wells, J. Kossin, C.-C. Wu, J. Hawkins.
1.1.1 Introduction
The purpose of this section is to describe advances in observational techniques (other than satellite systems described in the keynote sessions) that have proven useful in research and forecasting of tropical cyclone (TC) structure and structure change, which includes intensity change. Most of this paper will discuss advances associated with airborne radar or other remote sensors because the research aircraft platform has allowed the documentation of the structural characteristics over a broad range of TCs. Ground-based radar techniques will be only briefly discussed, even though operational Doppler radar networks have been deployed in the U.S., Taiwan, Australia, Japan, and other countries.
This report is extracted from a review (Marks 2002) presented in the David Atlas Symposium at the American Meteorological Society annual meeting, and will be included in a forthcoming book. An abbreviated summary of some key technological developments in radar systems for observing tropical cyclones since 1989 is given in that review. That review also included radar studies of TC-related precipitation, but these aspects will be deferred to Topic 2. In this section, the focus is on these radar observations of the structure of the mature TCs that document significant asymmetric motions and clouds (precipitation) in addition to the better-known axisymmetric aspects. The ability to map the complete three-dimensional circulation of the TC from airborne Doppler radar on time scales of an hour has enabled a partitioning of the wind to examine the roles of asymmetries in studies of intensity change (and motion). The evolution of the vortex asymmetries is now recognized as a key to understanding the evolution and its interaction with its environment (e.g., Schubert et al. 1999; Moller and Montgomery 1999; Reasor et al. 2000). These aspects will be emphasized in this report.
- Basic structure revealed by radar observations
The basic TC cloud structure can be described in terms of a stationary band complex that consists of an eyewall, a principal rainband, connecting bands, and several secondary rainbands outside the eyewall (Willoughby et al. 1985; book chapter by Willoughby 1995 from IWTC-III). The principal rainband marks the outer boundary of the vortex inner core. Outside this rainband, streamlines converge into the band or are deflected around the inner core. A secondary wind maximum is typically observed in the principal band (e.g., Marks and Houze 1984; Barnes and Powell 1995; Samsury and Zipser 1996). The eyewall is the focus of the upward branch of the secondary circulation of the vortex (characterized by flow radially inward at low levels, upward in the eyewall, and radially outward at high levels)(e.g., Willoughby et al. 1992; Jorgensen 1984a, b). The secondary rainbands are smaller than the principal rainband and tend to be embedded in regions of stratiform precipitation surrounding the eyewall. Outside convective cells, reflectivities are weaker, 30 dBZ, which is equivalent to a 2.4 mm h-1 rain rate. This “stratiform rain”, denoted by a distinct reflectivity maximum or “bright band” at the altitude of the 0_C isotherm falls out of the anvil cloud that grows from the convection. No wind maxima are found in these secondary rainbands and the vertical velocity is weak. The connecting band is a special form of the secondary bands. It is characterized by weak reflectivity and little vertical motion. One or more connecting bands are found between the downwind portion of the principal band and the eyewall.
Willoughby et al. (1984a) noted that concentric eyewalls may be found inside of the principal rainband in strong storms (maximum winds >50 m s-1 with large inner core circulations. The outer eyewall contains a secondary wind maximum with the same characteristic circulation and structure as the inner eyewall. The outer eyewall often contracts inward with time, eventually replacing the inner eyewall. In such an eyewall replacement cycle, the intensity first decreases and then increases again as the eyewall radius decreases.
The radial variation of the vertical reflectivity structure of the vertical velocity from vertical incidence Doppler observations within the inner 200 km of a TC is similar to that of a mature mesoscale convective system (MCS). The inner edge of the eyewall at altitudes from near the surface to the storm top is characterized by upward values as high as 20 m s-1, and median values of 3-4 m s-1 (e.g., Marks and Houze 1987; Black et al. 1996). Weak downdrafts are found generally below 6 km altitude coincident with the maximum eyewall reflectify, while the strongest downdrafts, as high as –15 m s-1, generally occur at altitudes >8 km (Black et al. 1994; Black et al. 1996). Outside the eyewall, the vertical velocities are much weaker, with weak ascent found above the height of the bright-band, and weak descent below the bright- band (e.g., Marks and Houze 1987; Black et al. 1996). Stronger vertical velocities can be found in strong rainbands, such as the secondary eyewall.
- Inner core structure from radar observations
Airborne Doppler data that are collected from two nearly orthogonal flight legs can be combined in a “pseudo” (using data from the same radar at two different times) or true dual-Doppler analysis of the three-dimensional wind field. The derived Doppler wind field covers horizontal and vertical dimensions of ~75-100 km and 15 km, respectively. The three-dimensional wind analyses are then possible in 0.5-1.0 h intervals (equivalent to a one-dimensional sample of flight-level winds 200-400 km in length), compared with the 4-6 h needed for the composite analyses of flight-level data. Hence, storm structure on scales of 20 km and 0.5-1.0 h, and particularly asymmetries that were difficult to infer from the composite analyses can now be deduced.
Marks et al. (1992) provided a framework by which the asymmetric nature of the inner core of a tropical cyclone can be described. The Doppler analysis of two tropical cyclones are used to illustrate this framework: Hurricanes Gilbert on 14 September 1988 (Dodge et al. 1999), and Hugo on 17 September 1989 (Roux and Marks 1996). The two storms provide a representative cross section of intensities and intensity change, where Hugo was a rapidly intensifying storm (central pressure falling at >2 mb h-1) with a central pressure of 952 hPa, while Gilbert was near peak intensity with a central pressure of 890 hPa for 12-18 h.
The three-dimensional wind field within each storm was derived from a “psuedo” dual-Doppler analysis using the NOAA WP-3D airborne Doppler radars. The flight legs used in the dual-Doppler analysis varied from 75-100 km in length (10-15 minutes). The average time separation between radial velocity estimates was 27 minutes, so that there was no possibility of deriving estimates of convective-scale motions. Because of limitations and differences in azimuthal and radial resolutions, these analyses concentrate on the mesoscale motions within the inner circulation (<100 km radius) with time scales of 45-60 minutes and space scales of wavenumber 2 in azimuth and 2-5 km in radius.
The horizontal relative wind vector 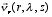 may be decomposed as
may be decomposed as
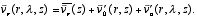 (1)
(1)
(i) (ii) (iii)
where (i) is the area-averaged storm-relative wind as a function of height, (ii) symmetric-vortex (wavenumber 0) circulation, and (iii) the asymmetric perturbation wind (wavenumber 1 and higher).
A key aspect of the wind partitioning is determining the center of the axisymmetric mean circulation at each altitude. The center is defined as the centroid of the inner core (radii <60 km) cyclonic vorticity maximum as defined by Marks et al. (1992). The circulation center for Hurricane Gilbert (Fig. 1.1.1a) varies 2-3 km with altitude and tilts from southwest to northeast with increasing altitude. Below 7 km altitude, the center positions made a cyclonic spiral within 1 km of the mean circulation center. From 7-12 km, the center was displaced up to 2 km from the mean center, and made an anticyclonic spiral with increasing height. In the Hugo case (Fig. 1.1.1b), the magnitude of the deviation of the center with altitude was larger (~5 km), and also tilted from southwest to northeast in an anticyclonic spiral with increasing altitude. The small magnitude of the deviation center with altitude for these cases (<10 km) indicated that when viewed on the vortex scale (~100-300 km), the storm center would be nearly vertically aligned.
Hodographs of 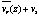 (Fig. 1.1.2) computed using (1) provide an estimate of the vertical shear of the flow in which the mean vortex is embedded. In both cases, the mean vertical shear in the lower troposphere is southwest to northeast, with a steady veering of the wind with increasing altitude, from easterlies at altitudes below ~5 km to southerlies or southwesterlies aloft. In both cases, the vortex center tilted in the direction of the mean shear from 1-10 km is less (5-6 m s-1) than that for Hugo case (9-10 m s-1), which suggests that the tilt of the vortex with height is related to the magnitude, as well as, the direction of the shear.
(Fig. 1.1.2) computed using (1) provide an estimate of the vertical shear of the flow in which the mean vortex is embedded. In both cases, the mean vertical shear in the lower troposphere is southwest to northeast, with a steady veering of the wind with increasing altitude, from easterlies at altitudes below ~5 km to southerlies or southwesterlies aloft. In both cases, the vortex center tilted in the direction of the mean shear from 1-10 km is less (5-6 m s-1) than that for Hugo case (9-10 m s-1), which suggests that the tilt of the vortex with height is related to the magnitude, as well as, the direction of the shear.
(a) (b)
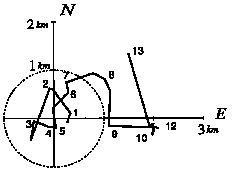
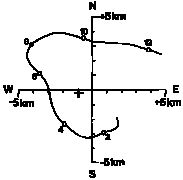
Fig. 1.1.1 Circulation centers at each level in the three-dimensional Doppler analyses for Hurricanes (a) Gilbert on 14 September 1988 and (b) Hugo on 17 September 1989. Positions are plotted relative to (a) the mean center of circulation in the first 6 km, which is 1.5 km west and 3.0 km north of the reflectivity center, and (b) the flight-level circulation center. The centers are plotted and labeled. The reference circle in (a) is 1 km in radius. The +-sign in (b) represents the density-weighted mean position (Dodge et al. 1999).
(a) (b)
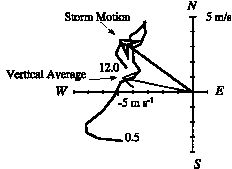
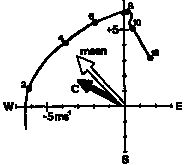
Fig. 1.1.2 Hodograph of mean winds from the three-dimensional Doppler analyses for Hurricanes (a) Gilbert on 14 September 1988 and (b) Hugo on 17 September 1989. Winds within 12-25 km from the center were averaged for each level up to 12 km altitude. The altitude of points in the hodograph is labeled where the lowest level in 0.5 km and the highest level is 12 km for both analyses. Arrows show the mean storm motion (denoted as C in (b)) and the density-weighted mean wind (vertical average), respectively (Dodge et al. 1999).
These two storms and the Norbert case studied by Marks et al.(1992) had similar storm motions, but distinctly different mean wind profiles. Norbert had a mean wind profile that was aligned along the direction of motion of the vortex, with 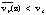 below 5 km altitude and
below 5 km altitude and 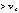 above that altitude. In contrast, both the Hugo and Gilbert cases had mean wind profiles aligned across the track. In Hugo (Fig. 1.1.2b), the mean wind was closest to the storm motion at 3 to 4 km altitude. In Gilbert (Fig. 1.1.2a), the mean wind was closest to the storm motion at 7 to 8 km altitude, which possibly indicates that Gilbert had a deeper vortex circulation. The magnitude of
above that altitude. In contrast, both the Hugo and Gilbert cases had mean wind profiles aligned across the track. In Hugo (Fig. 1.1.2b), the mean wind was closest to the storm motion at 3 to 4 km altitude. In Gilbert (Fig. 1.1.2a), the mean wind was closest to the storm motion at 7 to 8 km altitude, which possibly indicates that Gilbert had a deeper vortex circulation. The magnitude of 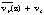 was never more than twice that of
was never more than twice that of 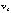 , which indicates that very little air was flowing through each vortex core (<100 km radius). In Hugo,
, which indicates that very little air was flowing through each vortex core (<100 km radius). In Hugo,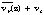 exceeded
exceeded 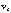 at all altitudes <10 km. In Gilbert,
at all altitudes <10 km. In Gilbert, 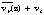 only exceeded
only exceeded 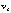 below 2 km and above 9 km altitude.
below 2 km and above 9 km altitude.
All three cases illustrate the effect vertical shear of the horizontal wind plays in vortex tilt. Each case indicates that the vortex tilts along the general direction of the shear vector with increasing height, with larger tilts associated with larger shear magnitude. These cases also point out the lack of a clear relationship between storm motion and vertical wind shear. Although all three storms had storm motions within 40_ of each other, they had drastically different shear patterns: along-track shear in Norbert, weak across-track shear in Gilbert, and relatively strong along-track shear in Hugo.
Marks et al. (1992) showed that in Norbert the vertical, mass-weighted average of the mean horizontal wind throughout the depth of the analysis derived from the partitioning agreed with synoptic analyses – lying about 20_ to the right of the storm motion. This mass-weighted mean wind in Gilbert (Fig. 1.1.2a) was to the left of the storm motion, while in Hugo (Fig. 1.1.2b) the mean was to the right of the storm motion. Similar deviations of the mean storm motion have been described in a number of studies (e.g., Neumann 1979; Chan 1986). These studies indicate that the storms tracking toward the northwest (Norbert and Hugo) tend to move faster than, and 10-20_ to the left of the mean flow, whereas storms moving more westerly (Gilbert) tend to move slower than and to the right of the mean flow.
(a) (b)

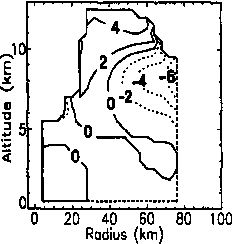
Fig. 1.1.3 radius-height mean of the radial flow from the three-dimensional Doppler analyses for Hurricanes (a) Gilbert, for the period 0902-1016 UTC 14 September 1988 (Dodge et al. 1999) and (b) Hugo for the period 2009-2055 UTC 17 September 1989 (Roux and Marks 1996). In (a) reflectivity (dBZ) is contoured in 5 dBZ contours starting at 15 dBZ, and the gray shades show the radial wind speed derived from the azimuthally averaged three-dimensional Doppler analysis. Black arrows map the secondary circulation; the vertical component was magnified two times to match the vertical scaling. The outflow regions are enclosed by a dashed line. In (b), contours represent the radial flow with solid contours corresponding to outflow and dashed contours inflow.
Another critical structural feature in the TC is the radial wind component of the symmetric vortex in Fig. 1.1.3. As with the tangential wind, both storm profiles have characteristics common to those described in the literature (e.g., Jorgensen 1984a, b; Marks and Houze 1987; Marks et al. 1992). They show weak symmetric radial flow inward or outward throughout most of the troposphere, except for a layer of outflow 4-8 m s-1 just outside the RMW above 8 km altitude. There is little evidence of a symmetric radial inflow in the lower troposphere primarily because of the lack of winds below 1 km altitude in both analyses. Hence, the vast majority of the inflow must be below that altitude. In contrast, the outflow layer near the RMW is rather deep, extending from 8-14 km altitude. In both cases, the mid-troposphere is characterized by weak inflow, where Gilbert (Fig. 1.1.3a) has weaker inflow than Hugo (Fig. 1.1.1b). The increased inflow in the Hugo case is likely related to the strengthening of the Hugo vortex at this time, whereas Gilbert was at peak intensity and slowly filling.
These radar-derived aspects of vortex tilt (Fig. 1.1.1), average wind with height (Fig. 1.1.2), and vertical wind shear in the vortex core (Fig. 1.1.3) are extremely difficult to measure via rawinsondes or other observation systems. They provide insights into the vertical structure of the inner core that should be compared with numerical model simulations in similar environmental flow conditions.
1.1.4 Asymmetric structure from radar observations
Marks et al. (1992) showed that in Hurricane Norbert the asymmetric perturbation field had a distinct signature at both lower and upper levels. At 1 km, the asymmetric perturbation had the form of a source-sink field. The source and sink were located at the radius of maximum winds (RMW) with the convergent sink on the leading, inflow side of the vortex and the divergent source on the trailing outflow side of the vortex. At 3 km and higher, the asymmetric wind fields had the character of a vortex couplet with cyclonic and anticyclonic perturbations in the right-front and left-rear quadrants of the storm, respectively, and stagnation points at the RMW on the upwind, trailing and downwind, leading side of the storm.
In Gilbert (Fig. 1.1.4a), the 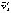 flow above 2 km is characterized by a wavenumber 1 vortex couplet aligned along the axis of the shear vector between 1-10 km altitude (Fig. 1.1.2). The vortex couplet is composed of a cyclonic perturbation in the downshear (right-front) quadrant and an anticyclonic perturbation in the upshear (left-rear) quadrant. The vortex couplet is centered on the RMW. As in the Norbert analysis, this couplet extends vertically from 2 km to the top of the vortex, and remains centered on the RMW as it slopes outward with increasing altitude. As in Norbert, the asymmetric perturbation below 2 km had the form of a source-sink field aligned along the direction of motion, similar to that described by Shapiro (1983).
flow above 2 km is characterized by a wavenumber 1 vortex couplet aligned along the axis of the shear vector between 1-10 km altitude (Fig. 1.1.2). The vortex couplet is composed of a cyclonic perturbation in the downshear (right-front) quadrant and an anticyclonic perturbation in the upshear (left-rear) quadrant. The vortex couplet is centered on the RMW. As in the Norbert analysis, this couplet extends vertically from 2 km to the top of the vortex, and remains centered on the RMW as it slopes outward with increasing altitude. As in Norbert, the asymmetric perturbation below 2 km had the form of a source-sink field aligned along the direction of motion, similar to that described by Shapiro (1983).
As found by Marks et al. (1992), the perturbations observed in Fig. 1.1.4 are much smaller in horizontal scale than those discussed by Willoughby (1988) and Fiorino and Elsberry (1989). The small-scale perturbations are contained entirely within the innercore region of the storm, centered at the RMW, and likely result from a nonlinear interaction between the mean vortex and the storm motion. Although the horizontal flow varied with altitude, the perturbations were nearly aligned in the vertical above the boundary layer, which suggests the interaction extended throughout the depth of the vortex.
(a) (b)

Fig. 1.1.4. The asymmetric perturbation wind (wavenumber 1 and larger) at 3 km altitude from the three-dimensional Doppler analyses for Hurricanes (a) Gilbert for the period 0902-1016 UTC 14 September 1988 and (b) Hugo for the period 1746-1947 UTC 17 September 1989. Reflectivity (dBZ)is contoured as shown, and the streamlines map the perturbation circulation (Marks 1991).
The relative importance of wavenumbers 0, 1, and 2 in terms of the explained variances in Hurricane Gloria (1985) had been studied by Lee et al. (1994). Wavenumber 0 (axisymmetric mean) dominated the explained variance and represented >90% of the variance at all radii. While the large explained variance of wavenumber 0 at radii >10 km suggests that the storm is relatively axisymmetric outside the RMW. The major asymmetries (wavenumbers 1 and 2) become important at and inside the RMW. It should be noted that the explained variance could be a result of the tangential or radial components in this case.
The relative importance of the wavenumbers 0, 1, and 2 tangential (VT) flow, and the wavenumbers 0 and 1 radial flow, in Hurricane Hugo is shown in Fig. 1.1.5. The amplitude of the wavenumber 0 tangential wind, VT-0 (Fig. 1.1.5a)is the largest over the whole domain, with maximum values >56 m s-1 at 30-40 km radii below 4 km altitude, which shows that the storm is dominated by a strong symmetric circulation. The symmetrical radial wind, VR-0 (Fig. 1.1.5b) is much smaller, especially below 5 km altitude, where it is <2 m s-1. Wavenumber 1 for the tangential wind VT-1 (Fig. 1.1.5c) has features similar to VT-0 with a maximum at the radius of VT-0, but with values a factor of seven smaller (<10 m s-1), as in the Gloria case. In contrast, the features associated with wavenumber 1 for the radial wind, VR-1 (Fig. 1.1.5d) are very different from those associated with VR-0 and are comparable in magnitude to VT-1. The maximum value (>6 m s-1) is larger and is found between 6-10 km altitude where VR-0 is small, which indicates that the secondary circulation is more complex than the primary one. The amplitude of wavenumber 2 for the tangential flow VT-2 (Fig. 1.1.5e) is everywhere smaller, with the maximum values >3 m s-1 at radii inside the maximum VT-0 (<25 km) below 5 km altitude, and at 60-80 km radii and 6-8 km altitude. A relative minimum of VT-2 is found at the location of the VT-0 and VT-1 maxima.
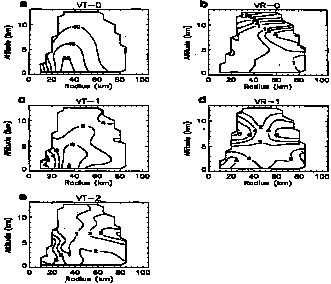
Fig. 1.1.5 Radius-height plot of the mean amplitude of the wind (m s-1) harmonics deduced from the three-dimensional Doppler analysis for Hurricane Hugo on 17 September 1989: (a)wavenumber 0 for the tangential wind (VT-0); (b) wavenumber 0 for the radial wind (VR-0); (c) wavenumber 1 for the tangential wind (VT-1); (d) wavenumber 1 for the radial wind (VR-1); and (e) wavenumber 2 for the tangential wind (VT-2)(Roux and Marks 1996).
Recognition of the relative importance of the wavenumber 0 to the mean horizontal wind and higher wavenumber components of the vortex wind field led to changes in perspective for numerical and dynamical studies, and also led to some new insights into vortex evolution and changes (e.g., Franklin et al. 1993; Liu et al. 1997, 1999; Viltard and Roux 1998; Shapiro and Montgomery 1993). Smith and Montgomery (1995) used these concepts to introduce vortex “axisymmetrization” into discussions on tropical cyclone dynamics. They pointed out that the observed angular velocity (V/r) changes from the core to the edge imply that the vortex time scale (defined as r/V) goes from 6-7 minutes (20 km/50 m s-1) near the center to 5-6 h (500 km/25 m s-1) in the periphery. This change in the rotational time scale results from increasing axisymmetrization as the flow reaches the core and the horizontal variability is forced into the radial direction. This dynamic control on the various fields has broad impacts on such diverse activities as vortex initialization in numerical models to understanding the rain distribution in the storm.
These studies also pointed out that while the axisymmetric mean explains the majority of the horizontal wind variance, intensity and track changes are dependent on the scale of the asymmetries, which are much weaker and harder to measure. The evolution of the vortex asymmetries are now recognized as the key to understanding the vortex evolution and its interaction with its environment (e.g., Schubert et al. 1999; Moller and Montgomery 1999; Reasor et al. 2000). Before advances can be made in tropical cyclone intensity change, a better understanding of the temporal variability of the asymmetries is needed.
- Case study of wind component change in rapid environmental shear change
The asymmetric dynamics of the tropical cyclone inner-core region were examined through a novel analysis of high temporal resolution, three-dimensional wind fields in Hurricane Olivia (1994), which were derived from true-dual Doppler radar analyses of airborne dual-Doppler radar data (Reasor et al 2000). Roux and Viltard (1995) had available a similar set of data for Hurricane Claudette (1991) that spanned a period of about 7 h. In the Olivia case, two NOAA WP-3D aircraft equipped with Doppler radar flew simultaneous, near-orthogonal flight tracks through the inner core on 25 September 1994. The use of two tail radar platforms allowed for true dual-Doppler sampling to be employed out to a radius of 30 km. The upper and lower aircraft flew through the inner core (radii <100 km) and provided near-simultaneous measurements of the horizontal wind components over a period of 10-15 minutes. Seven consecutive composites of Olivia’s wind field (Fig. 1.1.6) that were made during the period 2027-2355 UTC with 30-minute time resolution depict a weakening storm undergoing substantial structural changes. To focus on the symmetric and asymmetric components of the vortex wind separately, and to obtain insight into the dynamics governing the evolution of these components of the total flow, an azimuthal Fourier decomposition of the wind field following Marks et al. (1992) was performed.
The observations provide a unique look at the role of vertical shear in producing structural changes to the inner-core wind field. The seven consecutive area-averaged storm-relative wind 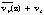 in Fig. 1.1.6 capture for the first time the asymmetric response of a tropical cyclone to dramatic changes in vertical shear over a relatively short time period. Initially the maximum local vertical shear over the 0.75-10.5-km depth is weak west-northwesterly, with values on the order of 3-5 m s-1. Consistent with the weak shear, the vortex was nearly vertically aligned (cf., Fig. 9 in Reasor et al. 2000). Over the next 2.5 h, the maximum shear increased from the west to 15 m s-1. A west-to-east tilt of the vortex with height evolved over the same time, with a maximum displacement from low to middle levels of about 3 km. Inspection of the flow field from 6 to 10.5 km height indicated that the inner core did not tilt more than 5 km.
in Fig. 1.1.6 capture for the first time the asymmetric response of a tropical cyclone to dramatic changes in vertical shear over a relatively short time period. Initially the maximum local vertical shear over the 0.75-10.5-km depth is weak west-northwesterly, with values on the order of 3-5 m s-1. Consistent with the weak shear, the vortex was nearly vertically aligned (cf., Fig. 9 in Reasor et al. 2000). Over the next 2.5 h, the maximum shear increased from the west to 15 m s-1. A west-to-east tilt of the vortex with height evolved over the same time, with a maximum displacement from low to middle levels of about 3 km. Inspection of the flow field from 6 to 10.5 km height indicated that the inner core did not tilt more than 5 km.
Black et al. (2002) show that the eyewall reflectivity (Fig. 1.1.7) became increasingly asymmetric as the vertical shear strengthened, such that the high reflectivity region shifted to the left of the shear on the northern side of the eyewall (Fig. 1.1.7b). During the ~3.5 h between the first image (2021-2058 UTC) and the last (2334-2413 UTC), the outer rings of high reflectivity largely disappeared, so that convection in the northern eyewall was the dominant reflectivity feature of the storm. As the outer convection weakened, the outer wind maxima disappeared. By 2300 UTC, vigorous convective cells in the northern eyewall grew to large horizontal extent and exhibited reflectivities >50 dBZ. Black et al. (2002) showed that at flight level and in vertical incidence Doppler radar data an 8 m s-1 updraft occupied the downshear (eastern) side of the eyewall and a 5 m s-1 downdraft occupied the upshear (western) side. As the relative flow caused by increasing vertical shear penetrated into the core, the earlier pattern of asymmetric radial flow became more pronounced. At 3 km altitude, the radial inflow dominated on the downshear side and outflow on the upshear side as the storm moved relative to the surrounding low-level air.
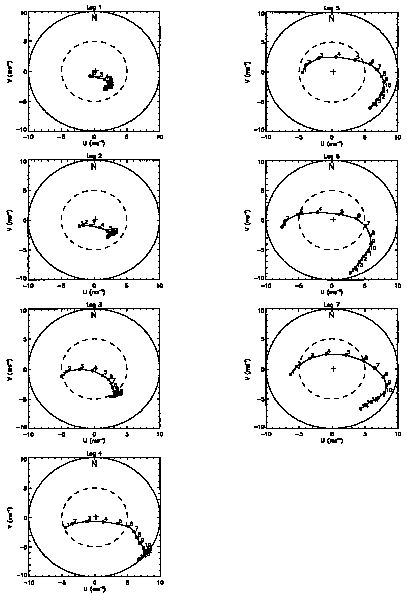
Fig. 1.1.6 Hodographs of the area-averaged storm-relative wind from 0.75 to 10.5 km height for each flight leg (seven legs, each roughly 30 minutes apart) in Hurricane Oliva (Reasor et al. 2002).
(a) (b)

Fig. 1.1.7 Lower fuselage radar composite of Hurricane Olivia on 25 September 1994 at (a) 2021-2058 UTC, and (b) for 2334-2413 UTC. The domain is 240 x 240 km square centered on the storm (Black et al. 2002).
The conceptual model by Black et al. (2002) for the environmental shear effect on a TC with opposing low-level and upper-level flows is presented in Fig. 1.1.8. Convective cells form somewhat upwind of the downshear side of the eyewall and advect around the eye into the semicircle to the left of shear vector where warm rain processes generate hydrometeors large enough to cause the maximum reflectivity region indicated. Precipitation-driven downdrafts begin about 90_ to the left of the shear vector. By the time the cells reach the upshear side of the eyewall they have ascended through the 0_C isotherm and downdrafts are predominantly below 6 km. As the cells move into the semicircle to the right of the shear vector, most of the condensate freezes or falls out of the active updrafts, and the “unloaded” updrafts accelerate upward, detach from the eyewall and approach the tropopause. These particles form the exhaust anvil in Fig. 1.1.8 as they rotate through the semicircle to the right of the shear. Clearly, such a conceptual model with a detailed description of the air flow through a TC in strong shear could only be produced from radar data.
Reasor et al. (2000) examined the observed weakening by 5-10 m s-1 just above the boundary layer trend by using axisymmetric vortex spindown ideas. The departure of the flow from cyclostrophic balance in the vortex boundary layer due to the presence of friction drives a radial inflow. This radial inflow transports angular momentum into the inner core, and compensates for the frictional losses of angular momentum. In the absence of diabatic forcing and the attendant radial inflow above the boundary layer, the free atmosphere radial flow will be outward at all levels (Willoughby 1979). By conservation of angular momentum, the tangential wind above the boundary layer must decrease, and the vortex spins down. Although inflow is still observed up to 3.5 km height, the flow above this level is outward at all radii and the time average symmetric radial flow over the 3.5 h observation period was outflow. This prevalence of radial outflow was also observed by Marks et al. (1992) for weakening Hurricane Norbert, as opposed to the weak inflow seen in intensifying or steady state storms such as Hurricanes Hugo and Gilbert (Fig. 1.1.3).
Fig. 1.1.8 Schematic by Black et al. (2002) of the shear-induced convective asymmetry near the TC eye based upon observations of Jimena and Olivia. The low-level environmental flow is indicated by the two solid black arrows. Upper-level flow is indicated by the three stippled arrows.
The evolution of Olivia’s vorticity derived from the dual-Doppler winds was also consistent with the vortex weakening. However, the vortex spindown may only be a partial explanation for the observed evolution. Such changes to the vorticity profile can also occur through asymmetric mechanisms. For example, the interaction of convectively forced vortex-Rossby waves with the mean flow will lead to changes in the mean vorticity profile (e.g., Montgomery and Kallenbach 1997; Montgomery and Enagonio 1998; Moller and Montgomery 1999). Nonlinear mixing of vorticity through the barotropic instability mechanism will also erode sharp radial gradients of symmetric vorticity.
The role of asymmetric vorticity dynamics in explaining some of the physics of tropical cyclone intensity change motivated a special focus on Olivia’s vorticity structure. Understanding the influence of vortex-scale dynamics on the distributon of convection and vorticity in the tropical cyclone inner core should aid in the prediction of the structure and evolution of a tropical cyclone as it enters, or is embedded in, different environmental flows. Fig. 1.1.9 shows that the vorticity takes the form of a ring of high values (12 x 10-3 s-1) centered on the RMW (9.5 km radius), and drops off sharply at larger radii with a hint that it drops below 8 x 10-3 s-1 at smaller radii. This vorticity structure resembles that presented in Schubert et al. (1999) for a hurricane-like vorticity ring. They predicted that some of the high vorticity
(a) (b)


Fig. 1.1.9 Tail radar reflectivity composite (shading dBZ) and (a) total vorticity (contours, 10-3 s-1) at 1 km altitude and (b) wavenumber one vorticity perturbation (shading, 10-3 s-1) and vertical velocity (contours m s-1) at 6 km altitude for Hurricane Olivia on 25 September 1994 at 2244-2255 UTC (leg 5). Solid contours represent positive w-values and dashed contours negative w-values.
of the ring is ultimately mixed into the center of the tropical cyclone vortex, and forms a monotonic symmetric vorticity profile. High vorticity is also ejected outward in the form of vortex Rossby waves (e.g., Montgomery and Kallenbach 1997).
A clear relationship exists between the mesoscale asymmetry in convection, which is likely forced by the vertical shear of the environmental winds, and the asymmetric pattern of reflectivity (Fig. 1.1.6) and vorticity (Fig. 1.1.9). The largest values of reflectivity occur immediately downwind of the regions of enhanced convection, which is consistent with hydrometeors being carried up by the updrafts of the convective cells and simultaneously swept downwind by the much stronger primary circulation. Vertical shear increased dramatically during the observation period, and lead to a strong projection of the convection onto an azimuthal wavenumber 1 pattern oriented along the maximum vertical shear vector. These observations are consistent with recent numerical simulations of hurricane-like vortices in vertical shear (Jones 1995; DeMaria 1996; Bender 1997; Frank and Ritchie 1999).
The perturbation vorticity at 6 km height in Fig. 1.1.9b shows enhanced convection is also closely associated with wavenumber 1 vorticity features. The vertical velocity maximum is upwind of the wavenumber 1 vorticity perturbation. According to the adiabatic mechanism for vertical velocity production, the preferred location for enhanced convection due to vertical shear effects should be downshear right in the east to southeast quadrant of the storm. Olivia was moving to the north-northeast at about 5 m s-1 during this time, so enhanced asymmetric boundary layer convergence is also expected in the north-northeast quadrant (Shapiro 1983). However, the upward velocity in Fig. 1.1.9b is generally a maximum downshear. As the vertical shear and vortex tilt increased, the maxiumum upward velocity increased from 1-2 to 12-16 m s-1 and the pattern of convection became more asymmetric. The storm translation speed during the analysis period is relatively steady and the direction of motion changes gradually by only 10_. Hence it is unlikely that the dramatic changes in vertical motion could be attributed to the asymmetric boundary layer convergence described by Shapiro (1983).
Bibliography
Barnes, G. M., and M. D. Powell, 1995: Evolution of the inflow boundary layer of Hurricane Gilbert (1988). Mon. Wea. Rev., 123, 2348-2368.
Bender, M. A., 1997: The effect of relative flow on the asymmetric structure in the interior of hurricanes. J. Atmos. Sci., 49, 703-724.
Black, M. L., R. W. Burpee, and F. D. Marks, 1996: Vertical motion characteristics of tropical cyclones determined with airborne Doppler radial velocities. J. Atmos. Sci.., 53, 1887-1909.
Black, M. L., J. F. Gamache, F. D. Marks, C. E. Samsury, and H. E. Willoughby, 2002: Eastern Pacific Hurricanes Jimena of 1991 and Olivia of 1994:The effect of vertical shear on structure and intensity. Mon. Wea. Rev., 130, 2291-2312.
Chan, J. C.-L., 1986: Supertyphoon Abby—An example of present track forecast inadequacies. Wea. Forecasting, 1, 113–126.
DeMaria, M., 1996: The effect of vertical shear on tropical cyclone intensity change. J. Atmos. Sci., 53, 2076-2087.
Dodge, P. P., R. W. Burpee, and F. D. Marks, 1999: The kinematic structure of a hurricane with sea level pressure less than 900 mb. Mon. Wea. Rev.,127, 987-1004.
Fiorino, M., and R. L. Elsberry, 1989: Some aspects of vortex structure related to cyclone motion. J. Atmos. Sci., 46, 975-990.
Frank, W. M., and E. A. Ritchie, 1999: Effects of environmental flow upon tropical cyclone structure. Mon. Wea. Rev., 127, 2044-2061.
Franklin, J. L., S. J. Lord, S. E. Feuer, and F. D. Marks, 1993: The kinematic structure of Hurricane Gloria (1985) determined from nested analyses of dropwindsonde and Doppler radar data. Mon. Wea. Rev., 121, 2433-2451.
Jones, S. C., 1995: The evolution of vortices in vertical shear: Initially barotropic vortices. Quart. J. Roy. Meteor. Soc., 121, 821-851.
Jorgensen, D. P., 1984a: Mesoscale and convective-scale characteristics of mature hurricanes. Part 1: General observations by research aircraft. J. Atmos. Sci., 41, 1268-1285.
Jorgensen, D. P., 1984b: Mesoscale and convective-scale characteristics of mature hurricanes. Part 11: Inner core structure of Hurricane Allen (1980). J. Atmos. Sci., 41, 1287-1311.
Lee, W.-C., R. Carbone, and F.D. Marks, 1994: Velocity track display-a technique to extract real-time tropical cyclone circulations using a single airborne Doppler radar J. Atmos. Ocean. Tech., 11, 337-356.
Liu, Y., D.-L. Zhang, and M. K. Yau, 1997: A multiscale numerical study of Hurricane Andrew (1992). Part I: Explicit simulation and verification. Mon. Wea. Rev., 125, 3073–3093.
Liu, Y., D.-L. Zhang, and M. K. Yau, 1999: A multiscale numerical study of Hurricane Andrew (1992). Part II: Kinematics and inner-core structures. Mon. Wea. Rev., 127, 2597–2616.
Marks, F., 2002: State of the Science: Radar view of tropical cyclones. Presented at the David Atlas Symposium, Amer. Meteor. Soc. Annual Meeting, Orlando, FL, 14 Jan 2002.
Marks, F. D., 1991: Kinematic structure of the hurricane inner core as revealed by airborne Doppler radar. Reprints of the 5th Conference on Mesoscale Processes, AMS, Atlanta, GA. 127-132.
Marks, F. D., and R. A. Houze, 1984: Airborne Doppler radar observations in Hurricane Debby. Bull. Amer. Meteor. Soc., 65, 569-582.
Marks, F. D., and R. A. Houze, and J. Gamache, 1992: Dual-aircraft investigation of the inner core of Hurricane Norbert: Part 1: Kinematic structure. J. Atmos. Sci., 49, 919-942.
Moller, J. D., and M. T. Montgomery, 1999: Vortex Rossby waves and hurricane intensification in a barotropic model. J. Atmos. Sci., 56, 1674-1687.
Montgomery, M. T, and R. Kallenbach, 1997: A theory for vortex Rossby-waves and its application to spiral bands and intensity changes in hurricanes. Quart. J. Roy. Meteor. Soc., 123, 435-465.
Montgomery, M. T, and J. Enagonio, 1998: Tropical cyclogenesis via onvectively forced vortex Rossby waves in a three- dimensional quasigeostrophic model. J. Atmos. Sci., 55, 3176-3207.
Neumann, C. J., 1979: On the use of deep-layer-mean geopotential height fields in statistical prediction of tropical cyclone motion. Sixth Conference on Probability and Statistics in Atmospheric Sciences, Banff, Alberta, AMS, 32-38.
Reasor, P. D., M. T. Montgomery, F. D. Marks, and J. F. Gamache, 2000: Low-wavenumber structure and evolution of the hurricane inner core observed by airborne dual-Doppler radar. Mon. Wea. Rev., 128, 1653-1680.
Roux, R. and N. Viltard, 1995:
Structure and evolution of Hurricane Claudette on 7 September 1991 from airborne Doppler radar observations. Part I Kinematics Mon. Wea. Rev., 123, 2611-2639.
Roux, F., and F. D. Marks, 1996: Extended velocity track display (EVTD): An improved processing method for Doppler radar observations of tropical cyclones. J. Atmos. Oceanic Technol., 13, 875-899.
Samsury, C. E., and E. J. Zipser, 1995: Secondary wind maxima in hurricanes: Airflow and relationship to rainbands. Mon. Wea. Rev., 123, 3502-3517.
Schubert, W. H., M. T. Montgomery, R. K. Taft, T. A. Guinn, S. R. Fulton, J. P. Kossin, and J. P. Edwards, 1999: Polygonal eyewalls, asymmetric eye contraction and potential vorticity mixing in hurricanes. J. Atmos. Sci., 56, 1197-1223.
Shapiro, L. J., 1983: The asymmetric boundary layer flow under a translating hurricane. J. Atmos. Sci., 40, 1984-1998.
Shapiro, L. J., and M. T. Montgomery, 1993: A three-dimensional balance theory for rapidly rotating vortices. J. Atmos. Sci., 50, 3322-3335.
Smith, G. B., and M. T. Montgomery, 1995: Vortex axisymmetrization: Dependence on azimuthal wavenumber or asymmetric radial structure changes. Quart. J. Roy. Meteor. Soc., 121, 1615-1650.
Viltard, N., and F. Roux, 1998: Structure and evolution of Hurricane Claudette on 7 September 1991 from airborne Doppler radar observations. Part II Thermodynamics Mon. Wea. Rev., 126, 281-302.
Willoughby, H. E., 1988: The dynamics of the tropical cyclone core. Aust. Meteor. Mag., 36, 193-191.
Willoughby, H. E., 1995: Mature structure and evolution. Chap. 2. Global Perspectives on Tropical Cyclones. (R. L. Elsberry, Ed.), WMO/Td-No. 393, World Meteorological Organization, 21-62.
Willoughby, H. E., F. D. Marks, and R. J. Feinberg, 1984: Stationary and propagating convective bands in asymmetric hurricanes. J. Atmos. Sci., 41, 3189-3211.
Willoughby, H. E., D. P. Jorgenson, R. A. Black, and S. L. Rosenthal, 1995: Project Stormfury: A scientific chronicle 1962-1983, Bull. Amer. Meteor. Soc., 66, 505-514.
Willoughby, H. E., J. Clos, and M. Shoribah, 1982: Concentric eyewalls, secondary wind maxima, and the evolution of the hurricane vortex. J. Atmos. Sci., 39, 395 -411.
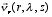 may be decomposed as
may be decomposed as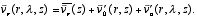 (1)
(1)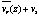 (Fig. 1.1.2) computed using (1) provide an estimate of the vertical shear of the flow in which the mean vortex is embedded. In both cases, the mean vertical shear in the lower troposphere is southwest to northeast, with a steady veering of the wind with increasing altitude, from easterlies at altitudes below ~5 km to southerlies or southwesterlies aloft. In both cases, the vortex center tilted in the direction of the mean shear from 1-10 km is less (5-6 m s-1) than that for Hugo case (9-10 m s-1), which suggests that the tilt of the vortex with height is related to the magnitude, as well as, the direction of the shear.
(Fig. 1.1.2) computed using (1) provide an estimate of the vertical shear of the flow in which the mean vortex is embedded. In both cases, the mean vertical shear in the lower troposphere is southwest to northeast, with a steady veering of the wind with increasing altitude, from easterlies at altitudes below ~5 km to southerlies or southwesterlies aloft. In both cases, the vortex center tilted in the direction of the mean shear from 1-10 km is less (5-6 m s-1) than that for Hugo case (9-10 m s-1), which suggests that the tilt of the vortex with height is related to the magnitude, as well as, the direction of the shear.



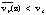 below 5 km altitude and
below 5 km altitude and 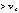 above that altitude. In contrast, both the Hugo and Gilbert cases had mean wind profiles aligned across the track. In Hugo (Fig. 1.1.2b), the mean wind was closest to the storm motion at 3 to 4 km altitude. In Gilbert (Fig. 1.1.2a), the mean wind was closest to the storm motion at 7 to 8 km altitude, which possibly indicates that Gilbert had a deeper vortex circulation. The magnitude of
above that altitude. In contrast, both the Hugo and Gilbert cases had mean wind profiles aligned across the track. In Hugo (Fig. 1.1.2b), the mean wind was closest to the storm motion at 3 to 4 km altitude. In Gilbert (Fig. 1.1.2a), the mean wind was closest to the storm motion at 7 to 8 km altitude, which possibly indicates that Gilbert had a deeper vortex circulation. The magnitude of 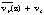 was never more than twice that of
was never more than twice that of 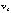 , which indicates that very little air was flowing through each vortex core (<100 km radius). In Hugo,
, which indicates that very little air was flowing through each vortex core (<100 km radius). In Hugo,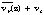 exceeded
exceeded 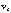 at all altitudes <10 km. In Gilbert,
at all altitudes <10 km. In Gilbert, 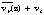 only exceeded
only exceeded 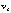 below 2 km and above 9 km altitude.
below 2 km and above 9 km altitude.

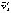 flow above 2 km is characterized by a wavenumber 1 vortex couplet aligned along the axis of the shear vector between 1-10 km altitude (Fig. 1.1.2). The vortex couplet is composed of a cyclonic perturbation in the downshear (right-front) quadrant and an anticyclonic perturbation in the upshear (left-rear) quadrant. The vortex couplet is centered on the RMW. As in the Norbert analysis, this couplet extends vertically from 2 km to the top of the vortex, and remains centered on the RMW as it slopes outward with increasing altitude. As in Norbert, the asymmetric perturbation below 2 km had the form of a source-sink field aligned along the direction of motion, similar to that described by Shapiro (1983).
flow above 2 km is characterized by a wavenumber 1 vortex couplet aligned along the axis of the shear vector between 1-10 km altitude (Fig. 1.1.2). The vortex couplet is composed of a cyclonic perturbation in the downshear (right-front) quadrant and an anticyclonic perturbation in the upshear (left-rear) quadrant. The vortex couplet is centered on the RMW. As in the Norbert analysis, this couplet extends vertically from 2 km to the top of the vortex, and remains centered on the RMW as it slopes outward with increasing altitude. As in Norbert, the asymmetric perturbation below 2 km had the form of a source-sink field aligned along the direction of motion, similar to that described by Shapiro (1983).

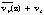 in Fig. 1.1.6 capture for the first time the asymmetric response of a tropical cyclone to dramatic changes in vertical shear over a relatively short time period. Initially the maximum local vertical shear over the 0.75-10.5-km depth is weak west-northwesterly, with values on the order of 3-5 m s-1. Consistent with the weak shear, the vortex was nearly vertically aligned (cf., Fig. 9 in Reasor et al. 2000). Over the next 2.5 h, the maximum shear increased from the west to 15 m s-1. A west-to-east tilt of the vortex with height evolved over the same time, with a maximum displacement from low to middle levels of about 3 km. Inspection of the flow field from 6 to 10.5 km height indicated that the inner core did not tilt more than 5 km.
in Fig. 1.1.6 capture for the first time the asymmetric response of a tropical cyclone to dramatic changes in vertical shear over a relatively short time period. Initially the maximum local vertical shear over the 0.75-10.5-km depth is weak west-northwesterly, with values on the order of 3-5 m s-1. Consistent with the weak shear, the vortex was nearly vertically aligned (cf., Fig. 9 in Reasor et al. 2000). Over the next 2.5 h, the maximum shear increased from the west to 15 m s-1. A west-to-east tilt of the vortex with height evolved over the same time, with a maximum displacement from low to middle levels of about 3 km. Inspection of the flow field from 6 to 10.5 km height indicated that the inner core did not tilt more than 5 km.


