WMO/CAS/WWW
FIFTH INTERNATIONAL WORKSHOP on TROPICAL CYCLONES
Topic 2.5: Storm Surge
Rapporteur: S. K. Dube
Indian Institute of Technology
Kharagpur 721 302
INDIA
E-mail: skdube@iitkgp.ernet.in
Fax: 91-3222-82000
Working Group: Reggina Garza, Issac Ginis, Tom Hardy, Lynn Shay, Edward Walsh
Abstract:
This report describes progress and improvements of the storm surge models (including inland inundation). Developments are proposed in effective operational numerical storm surge prediction facility for forecasting the total water level by including nonlinear interaction of wind waves and astronomical tides. A key component of the recommendation is capacity building and human resources development in the region of the vulnerable nations through training, provision of transfer of technology, and workshops / seminars.
2.5.1: Introduction
Storm surges are oscillations in the period range of a few minutes to a few days of the water level in a coastal or inland water body that result from forcing from the atmospheric weather systems. By this definition, the so-called wind-generated waves (often referred to as wind waves) and swell, which have periods of the order of a few to several seconds, are excluded. The term ”storm surge” is commonly used world-wide in scientific literature. In North American literature, the terms ”wind tides” and ”storm tides” are also used to refer to the same phenomenon.
The storm surge problem is an air-sea interaction problem; i.e. the atmosphere forces the water body, which responds by generating oscillations of the water level with various frequencies and amplitudes. Our present interest is confined to that part of the oscillation between a few minutes and a few days.
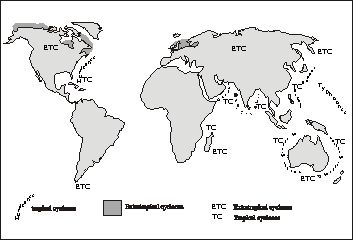
Coastal regions of countries are threatened by the possibility of storm surge floods whenever a tropical cyclone approaches. Figure 1 shows the regions of the globe affected by storm surges due to Tropical Cyclones (TCs) and Extra- tropical Cyclones (ETCs).

Figure 1: Coastal regions subjected to global storm surges due to Tropical Cyclones (TCs) with various localities and Extratropical Cyclones (ETCs).
The damage from landfalling cyclones is mainly due to three factors: rain, strong winds, and storm surges. Storm surges associated with severe tropical cyclones are by far the most damaging. Death and destruction arise directly from the intense winds that are characteristic of tropical cyclones blowing over a large surface of water. If bounded by a shallow basin, these winds cause the sea water to pile up on the coast and lead to sudden inundation and flooding of coastal regions. About 90% of the damage is due to inundation of land by sea water. In addition, flooding of the river deltas occur from the combined effects of tides and surges from the sea that penetrates into the rivers, because at the same time excess water in the rivers due to heavy rains from the cyclone is trying to flow through the rivers into the sea. Most of the world's greatest human disasters associated with the tropical cyclones have been directly attributed to storm surges. Thus, the real-time monitoring and warning of storm surge is of great concern. It is necessary that the problem of the storm surge be seriously addressed by the countries of the various regions through collective efforts and in an integrated way.
It may be noted that prediction of storm surge amplitude and extent of coastal inundation depend critically on the prediction of track (landfall) and intensity of tropical cyclones. Progress has been made in cyclone forecasting and warning during the last two decades under regional projects on tropical cyclones. The same cannot be said about the procedure for storm surge forecasting and warning. It is still inadequate. Cyclone forecasting must be further improved, and applied to drive models for forecasting storm surges. There are several aspects of the cyclone and storm surge warning systems and the disaster mitigation that require considerable improvements so as to bring about better response and minimize the loss of life and property.
Numerical storm surge prediction models are based on vertically integrated hydrodynamic equations governing the motion in the sea. The numerical solution procedure is either finite difference or finite element descretization of the equations.
Since the nonlinear advection terms have significant effect on the final results, especially in the shallow coastal waters, for operational applications the nonlinear terms cannot be left out. Thus, the models are preferably nonlinear and are forced by wind stress and by quadratic bottom friction. The treatment of the coastal boundaries in the most of the models involves a procedure that leads to a realistic representation of coastal boundaries and incorporates a detailed bathymetric specification in the important coastal regions.
2.5.3 Data input for surge prediction models
To achieve greater confidence in surge prediction, one should have a good knowledge of the input parameters for the model. These parameters include the oceanographic parameters, meteorological parameters (including storm characteristics), hydrological input, basin characteristics and coastal geometry, wind stress and seabed friction, and information about the astronomical tides. In many cases, these input parameters strongly influence the surge development. A brief account of these data input is given in the following sections:
a) Meteorological Input
This is mainly concerned with the characteristics of the tropical storms required for computation of the associated winds. The main characteristics required are:
(i) The pressure drop (difference between ambient pressure surrounding the storm and the central pressure),
(ii) vector motion of the storm,
(iii) place of landfall,
(iv) duration of the storm,
(v) maximum sustained winds, and
(vi) the radius of maximum wind.
Variables (i), (v), and (vi) typically must be estimated from satellite imagery. The variables (ii), (iii), and (iv) are obtained from the forecasts by the National Weather Services/ Weather Bureau.
Variables (i), (v), and (vi) of tropical cyclone are needed for the computation of the cyclone wind field, which is the foremost requirement for the computation of surges. Differing assumptions have been made by various workers (Murty et al. 1986) about the dependence of surface atmospheric pressure and wind speed on distance from the centre of the cyclone. One of the most important questions raised in this regard is whether or not any of these existing cyclone models give an accurate estimate of the associated wind field. Since the computation of storm surges is carried out by forcing the ocean model by the evolving wind stress distributions which is proportional to the square of the wind speed, any error in estimation of the wind may lead to substantial error in wind stress, and thus in the storm surge. Where no real-time, in-situ wind observations exist at the moment one has to live with these compromises. The best alternative would be to develop reliable numerical tropical cyclone structure prediction models by the meteorologists. No matter how accurately the storm structure is known or predicted, the track of the cyclone to the lanfall point must be accurately specified.
b) Oceanographic data
Data on oceanography are concerned with:
(a) Bathymetry
(b) Astronomical tides, and
(c) Inshore currents in closed regions.
Modelling experiments show that the surge is very sensitive to the basin depth. The shallowness of water may considerably modify the surge heights in the region. Therefore, accurate bathymetry maps are needed for improved surge prediction. Astronomical tides and the inshore currents also influence the surges through nonlinear interaction in the shallow water.
c) Basin characteristics and coastal geometry
The location of the highest surge depends predominantly on the coastal geometry of the basin. Experiments suggest that the curving coasts not only shift the peak surge position, but also affect its height (Dube et al. 1982). Modeling experiments by Johns et al. (1981) show that the surge is sensitive to the coastline representation.
d) Surface and bottom stress
The surface stress and sea-bed friction are usually parameterized by conventional quadratic wind or current law. Wind is the main generating mechanism of the surge; the height of the wave depends on the strength of the wind. Special care should be taken while computing the surface winds associated with a tropical cyclone.
e) Hydrological input
The main hydrological information needed is:
(i) River discharge in the sea, and
(ii) Rainfall distribution.
The simulations with river-ocean coupled mathematical models show that the discharge of fresh water carried by the rivers may modify the surge situation, especially in the northern Bay of Bengal where one of the world's largest river systems, the Ganga-Brahmaputra-Meghna, join the sea (Dube et al.1986). Another dynamic effect of these inlets and estuaries is the potentially deep inland penetration of the surge originating in the sea.
The impact of heavy precipitation associated with tropical cyclone on surge height has not been considered in the models for the Indian Seas. However, it is expected to influence the surge amplitude.
For the development of any forecasting storm surge model, one must take the above factors into consideration as far as possible.
2.5.4 Operational Storm Surge Prediction Models
Operational numerical storm surge prediction models have been developed and are being routinely used for several coastal regions of the world such as North Sea (Flather, 1976 and Flather and Proctor 1983), the Gulf of Mexico and Atlantic coast (Jelesnianski amd Chen 1979), Hong Kong, China, etc. Reviews of these models are given in Jiping et al. (1990), Jelesnianski (1989), Murthy (1984), and Sundermann and Lenz (1983).
Advent of powerful personal computers has set up a trend to run storm surge models in real-time on PC-based workstations in an operational office. In fact, a PC-based work station (the Automated Tropical Cyclone Forecasting System, ATCF) has already been operation at the Joint Typhoon Warning Centre, Hawaii for years. The Australian Bureau of Meteorology Research Centre, together with their Bureau Severe Weather Programme Office, has also developed an Australian workstation for storm surge forecasting. In India, Dube et al. (1994) developed a real-time storm surge prediction system for the coastal regions of India. Real-time storm surge prediction systems have also been developed for Bangladesh, Myanmar, and Sri Lanka.
The National Meteorological and National Hydrological Services of many countries have achieved some success in provision of storm surge warnings and for implementing improved models through co–operative and co–ordinated sharing of responsibilities within the framework and overall guidance and supervision of the Tropical Cyclone Programme (TCP) of the World Meteorological Organization (WMO). The TCP of WMO supported technology transfer to Bangladesh, Myanmar, and Sri Lanka from the Indian Institute of Technology-Delhi/Kharagpur. However, there are still several nations that still do not have expertise and resources to run an operational storm surge model.
2.5.5 Evaluation of Models
NASA and NOAA investigators are cooperating to develop an objective basis for evaluating the performance of storm surge models (Wright et al., 2002). The NASA Scanning Radar Altimeter (SRA) was designed primarily to measure the energetic portion of the directional wave spectrum (Wright et al., 2001; Walsh et al., 2002). It is being flown aboard a NOAA hurricane research aircraft to produce a sea-surface topographic map along the aircraft track. Figure 2 shows five contiguous 10-km segments of SRA gray-scale coded topography as the NOAA aircraft headed north toward Cape Hatteras (35.27oN, 75.44oW) during the landfall of Hurricane Bonnie on 26 August 1998. Time increases up the page and from left to right. The starting scan line number is indicated below each 10 km segment. The waves were just starting to encounter the continental shelf and feel the ocean floor at the beginning of this data segment, and the water depth decreased along the track. The waves were initially propagating toward about 335o. As the waves approached the shore, the wavelength shortened, the amplitude decreased, and the propagation direction turned toward the north and finally northeast. The surf zone began
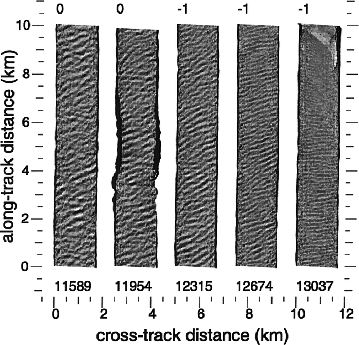
Figure 2: Gray-scale coded topographic map of the wave field south of Cape
Hatteras (35.27oN, 75.44oW) during the Hurricane Bonnie landfall.
at about 6.3 km up from the bottom of the right 10 km segment. The tip of Cape Hatteras is apparent at the top of the same segment.
Generating Figure 2 did not require an absolute determination of the height of the aircraft. The SRA swath is wide enough that each scan line can be processed independently and its mean elevation set to zero. But the SRA topographic map can be positioned absolutely in space using the Global Positioning System (GPS) in differential mode to determine the aircraft height. Determining the storm surge in this manner also characterizes the waves riding on top of the elevated mean water level, which provides much more information than can be obtained from a tide gauge.
The top panel of Figure 3 shows a storm surge hindcast for Hurricane Bonnie generated by the University of North Carolina at Chapel Hill (UNC), Institute of Marine Sciences Coastal Circulation and Transport Laboratory using the ADCIRC hydrodynamic model. The flight track of the NOAA aircraft is indicated by the thick line. The aircraft left the tip of Cape Lookout about 2213 UTC, followed the coastline down to Cape Fear, then proceeded due west, reaching the Myrtle Beach vicinity about 2250 UTC, and proceeding southwest along the shoreline for another 2 minutes before intersecting the beach. The absolute height of the aircraft was determined using the differential GPS
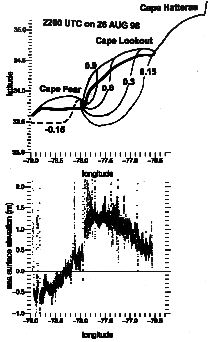
Figure 3: Storm surge model contours (m), NOAA aircraft track (thick line),
and sea surface elevation measured by the NASA SRA.
technique employing a ground station in addition to the aircraft receiver. The GPS height is relative to the ellipsoid, while the nominal mean water level would be relative to the geoid. The geoid displacement from the ellipsoid was determined from the GSFC00.1_MSS mean sea surface model in 2'x2' grid size, computed by combining satellite altimeter data of multi-missions (http://magus.stx.com/mssh/mssh.html). The mean sea surface model was interpolated to the position of each SRA scan line. The aircraft GPS height was corrected for the geoid displacement from the ellipsoid, the 4 m height difference between the GPS antenna on top of the aircraft and the SRA antenna on the bottom, and the effect of aircraft pitch changes on that height difference due to the SRA antenna being 4 m aft of the GPS antenna. The result is the absolute water level plot shown in the bottom panel of Figure 3 and registered to the longitude of the top panel. The model and observations are in good general agreement. This is remarkable considering that the up- and downdrafts in the hurricane caused the aircraft height to vary over a 120 m range during this flight line. Each dot in the bottom panel of Figure 3 indicates the sea surface height determined from a single SRA cross-track scan line. The vast majority of points are tightly clustered. The regions where the points spread or deviate from the general trend are easily explained when the wave topography is examined.
Because the SRA operates at 36 GHz, its signal is susceptible to attenuation by rain. The attenuation in dB is approximately linearly related to rain rate. At the 2.1 km height of the flight line shown in Figure 3, the SRA signal suffers a 1.17 dB attenuation for each mm/hr of rain rate. At lighter rain rates, this effect allows the determination of the path-integrated rain rate below the aircraft. At heavier rain rates the SRA signal margin is wiped out and the entire SRA signal lost. At 2.1 km height this occurs at about 10 mm/hr. Even with the 10 mm/hr rain rate limitation, relatively few data were lost along the flight line shown in Figure 3. Total loss of SRA signal due to rain occurred in the vicinity of 77.93oW and 78.12oW. There were several times along the flight line of Figure 3 when a partial loss of signal occurred because of rain, reducing the number of independent samples in the sea surface elevation computation. Abrupt and large roll maneuvers by the aircraft such as when it changes flight direction or is experiencing high turbulence also contaminate the SRA measurements. The places in Figure 3 where the SRA surface elevation data broaden significantly can be identified with these effects. Sophisticated editing algorithms are being developed, but these first-look data indicate great promise. At a 1 km height, the shorter path length would make the technique viable for rain rates up to 30 mm/hr.
The rapid transit of an aircraft and the ability to target the landfall area offers a more complete picture of the spatial characteristics of the surge than can be obtained from a few point measurements. The Hurricane Lili landfall in Louisiana on the U.S. Gulf coast on 3 October 2002 serves as an example. Figure 4 shows the track of Lili in the heavy dashes and the track of the NOAA aircraft carrying the SRA in the solid line. The aircraft provided excellent spatial coverage in the region where the surge was expected to be maximum, compared to the two nearest tide gauges, indicated by the “X”s at about 29.76oN, 93.34oW and 29.26oN, 89.96oW.
Figure 4: Hurricane Lili track (dash), NOAA aircraft track on 3 October
2002, and locations of nearest tide gauges (X).
The NASA Jet Propulsion Laboratory has developed the Internet-based Global Differential GPS (http://gipsy.jpl.nasa.gov/igdg/) which provides for GPS-based real-time positioning anywhere in the world without a ground station. It has routinely demonstrated a vertical accuracy of 20 cm. During recent flight tests, JPL achieved better than 10 cm vertical accuracy. This provides the possibility of making real-time storm surge measurements that could be assimilated into a model to provide immediate information on the actual spatial and temporal variation of the water level throughout the landfall region.
2.5.6 Recommendations
2.5.7 Summary
This report includes progress and improvements of the storm surge models (including inland inundation). Developments are proposed in effective operational numerical storm surge prediction facility for forecasting the total water level by including nonlinear interaction of wind waves and astronomical tides. A key component of the recommendation is capacity building and human resources development in the region of the vulnerable nations through training, provision of transfer of technology, and workshops / seminars.
Bibliography
Allen, S., (1998). Storm scenarios for 2100: Havoc on Mass coast, Private Communication.
Chittibabu, P., (1999). Development of storm surge prediction models for the Bay of Bengal and the Arabian Sea. Ph. D. Thesis, IIT Delhi, India, 262 pp.
Chittibabu, P., S. K. Dube, A. D. Rao, P. C. Sinha, and T. S. Murty, (2000). Numerical simulation of extreme sea levels using location specific high resolution model for Gujarat coast of India. Marine Geodesy, 23, 133-142.
Chittibabu, P., S. K. Dube, P. C. Sinha, A. D. Rao, and T. S. Murty, (2002). Numerical simulation of extreme sea levels for the Tamilnadu (India) and Sri Lanka coasts. Marine Geodesy 25, 235-244.
Druyan, L., and P. Lonergan, (1997). The impact of climate change on tropical cyclones. Risk Prediction Initiative Workshop, May 5-6, 1997, Hamilton, Bermuda.
Dube S.K., P.C. Sinha, and A.D. Rao (1982). The effect of coastal geometry on the location of peak surge. Mausam 33, 445-450.
Dube, S.K., P.C. Sinha, and G.D. Roy, (1986). Numerical simulation of storm surges in Bangladesh using a River - Bay coupled model. Coastal Engineering, 10, 85-101.
Dube, S.K., A.D. Rao, P.C. Sinha, and P. Chittibabu, (1994). A real-time storm surge prediction system: An application to east coast of India. Proc. Indian Natn. Sci. Acad. 60, 157-170.
Dube, S. K., (1998a). Mathematical modelling of storm surges associated with tropical cyclones. Proceedings of the National Seminar on Application of Mathematics in Industries and Environment, Agra, December 17-18. Chapter 4, 13-25.
Dube S.K., (1998b). Storm surge modelling and prediction in the Bay of Bengal: An application to Myanmar. Presented at MYANMAR – INDIA Workshop on Oceanography of Bay of Bengal and the Andaman Sea, 25 – 28 November 1998, Yangon, Myanmar, 16 p.
Dube, S. K., P. Chittibabu, P. C. Sinha, A. D. Rao, and T. S.Murty, (1999a). Storm surges and inundation on the Andhra Coast, India. In: Recent advances in Marine Science and Technology - 98, pp. 57-66.
Dube, S. K., P. Chittibabu, A. D. Rao, P. C. Sinha, and T. S. Murty, (2000a). Extreme sea levels associated with severe tropical cyclones hitting Orissa coast of India, Marine Geodesy, 23, 75-90.
Dube, S. K., P. Chittibabu, A. D. Rao, P. C. Sinha, and T. S. Murty, (2000b). Sea levels and coastal inundation due to tropical cyclones in Indian coastal regions of Andhra and Orissa. Marine Geodesy, 23, 65-73.
Dube, S.K., A.D.Rao, P.C.Sinha, and T.S.Murty, (1998). Storm Surges in the Bay of Bengal, In “Maritime Natural Hazards in the Indian Ocean Region” (Edited by: Colin D. Woodreffe), Wollongong University Press, 43-82.
Dube, S.K., A.D. Rao, P.C. Sinha, T.S.Murty, and N. Bahulayan, (1997). Storm surge in the Bay of Bengal and Arabian Sea: The problem and its prediction. Mausam 48, 283-304.
Dube, S. K., P. C. Sinha, A. D. Rao, and P. Chittibabu, (1999b). Recent developments in storm surge modeling and future trends. In Meteorology Beyond 2000 (Ed. A. K. Bhatnagar, S. Raghavan, R. N. Keshavamurthy, G. S. Ganesan, J. Shanmugasundram, S. Rajarathnam, N. Jayanthi, S. K. Subramanian, R. Suresh and Y. E. A. Raj), Indian Meteorological Society, Chennai, India. pp. 521-531.
Dube, S. K., A. D. Rao, P. C. Sinha, and P. Chittibabu, (2000c). Storm surge modeling and prediction, In Mathematical Analysis and Applications (Edited by: A. P. Dwivedi), Narosa Publishing House, New Delhi, India. pp. 109-124.
Dube S. K., P. Chittibabu, P. C. Sinha, A. D. Rao and T. S. Murty, (2002).Numerical modeling of storm surges in the head Bay of Bengal using location specific model. Natural Hazards 24 (2002).
Flather R.A., (1976). Practical aspects of the use of numerical models for surge prediction. Rep. No. 30, Inst. Ocean. Sci., Bidston, UK.
Flather R.A., and R. Proctor (1983). Prediction of North-Sea storm surges using numerical models: Recent developments in UK. In "North Sea Dynamics"(Ed. Suinderman/Lenz) Springer-Verlag, Berlin Heidelberg, 299-317.
Gönnert; G., (1998). Sturmfluten im Elbeästuars. In: Schriftenreihe der Niedersächsischen Akademie für Geowissenschaften, Heft 14, S.24-35.
Gönnert, G., (1999a). The analysis of storm surge climate change along the German coast during the 20th century. In: Journal of Quarternary International, S.115-121.
Gönnert, G., (1999b). Veränderung des Charakters von Sturmfluten in der Nordsee aufgrund von Klimaänderung in den letzten 100 Jahren. In: Marburger Geographische Schriften, 134, 24-39.
Gönnert, G., (1999c). Sturmfluthöhen in der Nordsee. Auswirkungen der Klimaänderung in den letzten 100 Jahren. In: Jahrbuch der Hafenbautechnischen Gesellschaft, 52, 192-201.
Gönnert, G., S. K. Dube, T. Murty, and W. Siefert, (2001). Global storm surges: theory, observations and applications. Die Kueste, pp. 623.
Gönnert, G., and W. Siefert, (1997). Storm surge development in the Sothern North Sea and the Elbe river in Europe during the last century and its practical application, Mausam, 48, 499-514.
Gönnert, G., and W. Siefert, (1998). Sturmflutatlas Cuxhaven. Hamburg, Strom- und Hafenbau. Studie Nr. 92. 1998.
Grassl, H., (1998). Nur aus Forschung zum globalen Wandel folgt Nachhaltigkeit. In. Geographische Rundschau, 5, 268-272.
Hagen, S.C., O. Horstman, and R.J. Bennett,(2002). “ An Unstructured Mesh Generation Algorithm for Shallow Water Modeling.” The International Journal of Computational Fluid Dynamics”, 16, 83-91.
Henry R. F., D. S. Duncalf, R. A. Walters, M. J. Osborne, and T. S. Murty, (1997). A study of tides and storm surges in offshore waters of the Meghna estuary using a finite element model. Mausam 48 (4), 519-530.
Hubbert, G. D., and K. L. McInnes, (1999). A storm surge inundation model for coastal planning and impact studies. Journal of Coastal Research, 15, 168-185.
Imamura F., and D. V. To, (1997). Flood and typhoon disasters in Vietnam in the half-century since 1950, Natural Hazards, 15, No. 1, 71-87.
Jelesnianski C.P., (1989). Storm surge and sea-state. Topic 5.2, Second International Workshop on Tropical Cyclones, Manila, December 1989. WMO/TD-No.319, WMO, Geneva, 277-293.
Jelesnianski C.P., and J. Chen (1979). SLOSH (Sea Lake and Overland Surges from Hurricanes). Report of TDL, NWS, Silver Spring, MD. 16pp.
Jelesnianski, C.P., J. Chen, and Shaffer W.A., (1992). “SLOSH: Sea, Lake, and Overland Surges from Hurricanes”, NOAA Technical Report NWS 48.
Jiping C., T.S. Murthy, B. Chenglan, M.I. El-Sabh, and L. Fengshu, (1990). Storm Surges: Observations and Modelling. China Ocean Press, 326pp.
Johns B., S.K. Dube, U.C. Mohanty, and P.C. Sinha, (1981). Numerical simulation of the surge generated by the 1977 Andhra Cyclone. Quart. J. Roy. Met. Soc.,107, 915-934.
Jones, J. E., and A. M. Davies, (1998). Storm surge computations for the Irish Sea using a three dimensional numerical model including wave – current interaction. Cont. Shelf. Res. 18, 201 – 251.
Kahlfeld, A., (1999). Numerische Seegangsmodellierung als Bestandteil einer funktionellen Hafenplanung. Dissertation. Institut für Strömungsmechanik und Elektronisches Rechnen im Bauwesen der Universität Hannover, Berichte, 58.
Kowalik, Z., and I. Polyakov, (1998). Tides in the Sea of Okhotsk. In: Journal of Physical Ozeanography, (20) 7, p.1389-1409.
Luick, J. L., R. F. Henry, and T. S. Murty, (1997). Storm surges in the Pacific Forum Region", In Recent advances in Marine Science and Technology-96, edited by N. K. Saxena, PACON International, Honolulu, 167-176
Mai, S., and K.F. Daemrich, and C. Zimmermann, (1997). Wellentransformation an Sommerdeichen. In: Wasser und Boden, 9.
Minato S., (1998). Storm surge simulation using POM and a revisitation of dynamics of sea-surface elevation short-term variation. Meteorology and Geophysics, 48, 79-88.
Murty T.S., (1984). Storm Surges. Meteorological Ocean Tide. Department of Fisheries and Oceans, Ottawa, Canada, 897p.
Murty, T. S., and S. K. Dube, (2000). Mitigation of Marine hazards in India, Proc. of the Indian Ocean Studies, 92-1114.
Murty, T.S., R.A. Flather, and R.F. Henry (1986). The storm surge problem in the Bay of Bengal. Prog. Oceanog.16, 195-233.
Prasad K. B., R. Kalra, S. K. Dube, P. C. Sinha, A. D. Rao, R. Kumar, and A. Sarkar, (2000).Extreme wave conditions over the Bay of Bengal during severe cyclone-Simulation experiment with two spectral wave models. Marine Geodesy, 23, 91-102.
Rabinovich A. B., and S. Monserrat, (1998). Generation of meteorological tsunamis (large amplitude seiches) near the Balearic Islands. Natural Hazards, 18, 27-55.
Rao, A.D., S.K. Dube, and P. Chittibabu, (1994). Finite difference techniques applied to the simulation of surges and currents around Sri Lanka and Southern Indian Peninsula. Comp. Fluid Dyn., 3, 71-77.
Rao, Y.R., P.Chittibabu, S.K. Dube, A.D. Rao, and P.C. Sinha, (1997). Storm surge prediction and frequency analysis for Andhra coast of India. Mausam 48, 555-566.
Rappaport, E. N., (2000). “Loss of life in the United States associated with recent Atlantic tropical cyclones.” Tropical Prediction Center, National Hurricane Center, NOAA/NWS, Miami, FL
Roy, G. D., (1999a). Inclusion of off-shore islands in a transformed coordinates shallow water model along the coast of Bangladesh. Environment International, 25, 67-74.
Roy, G. D., (1999b). Sensitivity of water level associated with tropical storms along the Meghna estuary in Bangladesh. Environment International, 25, 109-116.
Siefert, W., (1998). Bemessungswasserstände 2085A entlang der Elbe . Ergebnisse einer Überprüfung durch die Länderarbeitsgruppe nach 10 Jahren 1995/1996. In: Die Küste, Heft 60, 227-255..
Sinha, P. C., Y. R. Rao, S. K. Dube, and T. S. Murty, (1997). Effect of sea level rise on tidal circulation in Hooghly Estuary, Bay of Bengal. Marine Geodesy. 20, 341-366.
Sinha, P.C., Y.R. Rao, S.K. Dube, and A.D. Rao, (1996). Numerical investigation of tide-surge interaction in Hooghly estuary, India, Marine Geodesy. 19, 235-255.
Sinha, P. C., S. K. Dube, A. K. Mitra, and T. S. Murty (2000). A tidal flow model for the Gulf of Kachchh, India. Marine Geodesy, 23(2000) 117-132.
Sundermann J., and W. Lenz (1983). North Sea Dynamics, Springer-Verlag, Berlin. Heidelberg, 693 pp.
Thaw, S. H., (1998). Storm surges and status of prediction in Myanmar. Report to the Myanmar- India Workshop on Oceanography of the Bay of Bengal and the Andman Sea. November 25-28, 1998 Yangon, Myanmar, 19 pp.
Walsh, E. J., C. W. Wright, D. Vandemark, W. B. Krabill, A. Garcia, S. H. Houston, S. T. Murillo, M. D. Powell, P. G. Black, and, F. D. Marks, 2002: Hurricane directional wave spectrum spatial variation at landfall, J. Phys. Oceanogr., 32, 1667-1684.
Walsh, K., and A. B. Pittock, (1998). Potential changes in tropical storms, hurricanes, and extreme rainfall events as a result of climate change, Climate Change, 39, 199-213.
Walters, R. A., and V. Casulli, (1998). A robust, finite element model for hydrostatic surface water flows. Communications in Numerical Methods in Engineering, 14, 931-940.
Wang, X., and J. Wang, (1997). The calculation of maximum elevation due to storm surge by using joint probability method. Mausam, 48, 587-594.
Wright, C. W., E. J. Walsh, D. Vandemark, W. B. Krabill, A. Garcia, S. H. Houston, M. D. Powell, P. G. Black, and F. D. Marks, 2001: Hurricane directional wave spectrum spatial variation in the open ocean, J. Phys. Oceanogr., 31, 2472-2488.
Wright, C. W., E. J. Walsh, W. B. Krabill, D. Vandemark, A. W. Garcia, P. G. Black, F. D. Marks, Jr., R. A. Luettich, Jr., 2002: Real-time storm surge measurement with a scanning radar altimeter, IGARSS’02, Toronto, 24-28 June 2002.
Yamashita T., and G. Watson, (1997). Wind-wave-surge interaction prediction, In: Recent Advances in Marine Science and Technology, Ed. N. K. Saxena, PACON International, Honolulu, 153-165.