Updraft Effects on Z-R Relations

If we examine the effects of the significant downdrafts and updrafts separately, the downdrafts tend to shift the data points to a higher rainfall rate for a given Z. However, the effect is fairly small since there were virtually no large organized downdrafts in this sample (<w> < -2.0 m/s).

There were numerous significant updrafts, however, and their effect on the Z-R relations was to shift the data points so the resultant regression line is to the left of that for the whole population. To illustrate the effects of updrafts on the Z-R relations the sample was limited to the upper 5% (268 samples) of the 6-s mean <w> > 2.0 m/s.


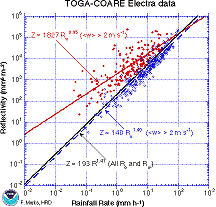
The measured updrafts reduced the resultant Rw values significantly. In some cases Rw actually became negative (all of the precipitation water is rising) and could not be plotted on the log scale. This was particularly true at low rainfall rates.

Because much of the rain is moving upward in updrafts, in convection we should consider the flux of precipitation, or rain water, and not rainfall rate per se. For example, for the 5% of points with <w>>2.0 m/s, the sum of the precipitation flux (sum R0, sum R w) changes from 4990.4 to 1240.1 mm/hr (i.e., only 25% of the rain is falling) upon the application of updraft velocity, and in a number of samples virtually all of the precipitation hydrometeors are rising. Moreover, the large mass of water which is rising will fall out later at places far removed from the measurement volume, the smaller the drops the further away. Of course, some of these small drops will not survive evaporation. The drop distributions will undergo significant evolution from their initial formation in convective updrafts and their complex trajectories to the surface.

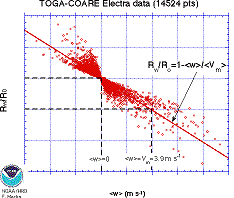
Another way of looking at the effect updrafts have on the resultant rainfall rate is by plotting <w> versus the ratio Rw/R 0.


When Rw/R0=0 the bulk of the rain is suspended. This occurs at the intercept <w>=3.9 m/s. The intercept is nearly equal to the mean and median <Vm> for the entire sample (3.7 m/s and 4.0 m/s, respectively). Most of the drop size distributions observed during TOGA COARE had a mean <Vm> in this range. Distributions of <Vm> and <w> for a given distribution can be used to determine whether a substantial portion of the rain mass is rising.

References

Atlas, D., P. Willis, and F. Marks, 1995: Draft effects upon reflectivity-rain rate relations. Proceedings of the 27th Conference on Radar Meteorology, Vail, CO, AMS.

Willis, P., R. Black, F. Marks, and D. Baumgardner, 1995: Airborne rain drop size distributions in TOGA COARE. Proceedings of the 21st Conference on Hurricanes and Tropical Meteorology, Miami, FL, AMS, 431-433.
marks@aoml.noaa.gov
Updated Thur, May 7, 1998